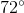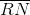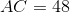All PSAT Math Resources
Example Questions
Example Question #1 : How To Find The Area Of A Hexagon
Calculate the approximate area a regular hexagon with the following side length:
Cannot be determined
How do you find the area of a hexagon?
There are several ways to find the area of a hexagon.
- In a regular hexagon, split the figure into triangles.
- Find the area of one triangle.
- Multiply this value by six.
Alternatively, the area can be found by calculating one-half of the side length times the apothem.
Regular hexagons:
Regular hexagons are interesting polygons. Hexagons are six sided figures and possess the following shape:
In a regular hexagon, all sides equal the same length and all interior angles have the same measure; therefore, we can write the following expression.

One of the easiest methods that can be used to find the area of a polygon is to split the figure into triangles. Let's start by splitting the hexagon into six triangles.

In this figure, the center point, 


We also know the following:
Now, let's look at each of the triangles in the hexagon. We know that each triangle has two two sides that are equal; therefore, each of the base angles of each triangle must be the same. We know that a triangle has 
Each angle in the triangle equals 



Let's solve for the length of this triangle. Remember that in 
Now, we can analyze 


We know the measure of both the base and height of 
Now, we need to multiply this by six in order to find the area of the entire hexagon.
We have solved for the area of a regular hexagon with side length, 
If we are not given a regular hexagon, then we an solve for the area of the hexagon by using the side length(i.e. 



Alternative method:
If we are given the variables 

In this equation, 




Solution:
In the given problem we know that the side length of a regular hexagon is the following:
Let's substitute this value into the area formula for a regular hexagon and solve.
Simplify.
Round the answer to the nearest whole number.
Example Question #591 : Geometry
What is the measure, in degrees, of one interior angle of a regular pentagon?
120
180
144
72
108
108
The formula for the sum of the interior angles of any regular polygon is as follows:
where 
Therefore, the sum of the interior angles for a regular pentagon is:
To find the measure of one interior angle of a regular pentagon, simply divide by the number of sides (or number of interior angles):
The measure of one interior angle of a regular pentagon is 108 degrees.
Example Question #1 : How To Find An Angle In A Pentagon

Refer to the above figure, which shows Square 

Evaluate 
By angle addition,



To find 



Also, since, in 


Since the angles of a triangle must total 
Example Question #1 : How To Find The Angle Of Two Lines

Refer to the above figure. You are given that 


I)
II) 

III) 
II and III only
I and III only
None of these
I, II, and III
I and II only
I and III only
If 




then, by the converse of the Pythagorean Theorem, 

If 






The correct response is Statement I and III only.
Example Question #591 : Geometry

Note:
Refer to the above diagram. 

Two angles formed by a transversal line crossing two other lines are corresponding angles if, relative to the points of intersection, they are in the same position. 





Example Question #1 : How To Find The Angle Of Two Lines

Refer to the above diagram. 


Two angles formed by a transversal line crossing two other lines are alternate interior angles if:
I) Both angles have their interiors between the lines crossed
II) The angles have their interiors on the opposite sides of the transversal.
Of the given choices, only 



Example Question #2 : Lines

Refer to the above diagram.

Two angles are vertical angles if they share a vertex, anf if their union is a pair of intersecting lines. Of the five choices, only 

Example Question #592 : Geometry

Refer to the above figure.
Which of the following segments is a diagonal of Pentagon 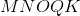
A diagonal of a polygon is a segment whose endpoints are nonconsecutive vertices of the polygon. Of the five choices, only 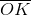
Example Question #1 : How To Find The Perimeter Of A Rhombus
If the area of a rhombus is 24 and one diagonal length is 6, find the perimeter of the rhombus.
24
12
20
16
8
20
The area of a rhombus is found by
A = 1/2(d1)(d2)
where d1 and d2 are the lengths of the diagonals. Substituting for the given values yields
24 = 1/2(d1)(6)
24 = 3(d1)
8 = d1
Now, use the facts that diagonals are perpendicular in a rhombus, diagonals bisect each other in a rhombus, and the Pythagorean Theorem to determine that the two diagonals form 4 right triangles with leg lengths of 3 and 4. Since 32 + 42 = 52, each side length is 5, so the perimeter is 5(4) = 20.
Example Question #1 : Quadrilaterals

Note: Figure NOT drawn to scale.
Calculate the perimeter of Quadrilateral 
Insufficient information is given to answer the question.



We focus on 
By the Pythagorean Theorem,
26 is the common length of the four sides of Quadrilateral 

Certified Tutor
Certified Tutor
All PSAT Math Resources



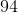












![\textup{Area of Hexagon}[ABCDEF]=6\times\frac{\sqrt{3}s^2}{4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1065143/gif.latex)
![\textup{Area of Hexagon}[ABCDEF]=\frac{6 \sqrt{3}s^2}{4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1065144/gif.latex)
![\textup{Area of Hexagon}[ABCDEF]=\frac{3\sqrt{3}}{2}\times s^2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1065145/gif.latex)