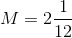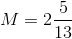All PSAT Math Resources
Example Questions
Example Question #1 : How To Find The Length Of The Side Of A Right Triangle
A right triangle has two sides, 9 and x, and a hypotenuse of 15. What is x?
10
12
13
14
11
12
We can use the Pythagorean Theorem to solve for x.
92 + x2 = 152
81 + x2 = 225
x2 = 144
x = 12
Example Question #11 : How To Find The Length Of The Side Of A Right Triangle
The area of a right traingle is 42. One of the legs has a length of 12. What is the length of the other leg?
Example Question #1 : How To Find The Length Of The Side Of A Right Triangle

If 


AB is the leg adjacent to Angle A and BC is the leg opposite Angle A.
Since we have a 

Here, we know the side opposite the sixty degree angle. Thus, we can set that value equal to 
which also means
Example Question #6 : How To Find The Length Of The Side Of A Right Triangle
Solve for x.
6
7
12
2
6
Use the Pythagorean Theorem. Let a = 8 and c = 10 (because it is the hypotenuse)
Example Question #461 : Geometry

Note: Figure NOT drawn to scale.
Refer to the above diagram. Evaluate 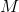
The altitude perpendicular to the hypotenuse of a right triangle divides that triangle into two smaller triangles similar to each other and the large triangle. Therefore, the sides are in proportion. The hypotenuse of the triangle is equal to
Therefore, we can set up, and solve for 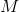
Example Question #461 : Psat Mathematics
What is the hypotenuse of a right triangle with sides 5 and 8?
√89
12
5√4
15
8√13
√89
Because this is a right triangle, we can use the Pythagorean Theorem which says a2 + b2 = c2, or the squares of the two sides of a right triangle must equal the square of the hypotenuse. Here we have a = 5 and b = 8.
a2 + b2 = c2
52 + 82 = c2
25 + 64 = c2
89 = c2
c = √89
Example Question #1 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem

If 


Not enough information to solve
This problem is solved using the Pythagorean theorem 



Using the labels of our triangle we have:
Example Question #2 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem
If one of the short sides of a 45-45-90 triangle equals 5, how long is the hypotenuse?
5
√10
5√2
√15
π
5√2
Using the Pythagorean theorem, x2 + y2 = h2. And since it is a 45-45-90 triangle the two short sides are equal. Therefore 52 + 52 = h2 . Multiplied out 25 + 25 = h2.
Therefore h2 = 50, so h = √50 = √2 * √25 or 5√2.
Example Question #3 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem
The height of a right circular cylinder is 10 inches and the diameter of its base is 6 inches. What is the distance from a point on the edge of the base to the center of the entire cylinder?
4π/5
None of the other answers
√(43)/2
√(34)
3π/4
√(34)
The best thing to do here is to draw diagram and draw the appropiate triangle for what is being asked. It does not matter where you place your point on the base because any point will produce the same result. We know that the center of the base of the cylinder is 3 inches away from the base (6/2). We also know that the center of the cylinder is 5 inches from the base of the cylinder (10/2). So we have a right triangle with a height of 5 inches and a base of 3 inches. So using the Pythagorean Theorem 32 + 52 = c2. 34 = c2, c = √(34).
Example Question #2 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem
A right triangle with sides A, B, C and respective angles a, b, c has the following measurements.
Side A = 3in. Side B = 4in. What is the length of side C?
6
9
7
25
5
5
The correct answer is 5. The pythagorean theorem states that a2 + b2 = c2. So in this case 32 + 42 = C2. So C2 = 25 and C = 5. This is also an example of the common 3-4-5 triangle.
All PSAT Math Resources