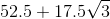Every triangle has 180 degrees.  An isosceles triangle has one vertex angle and two congruent base angles. 

Solve the equation for x to find the measure of the vertex angle. 

x = 180 - 27 - 27

x = 126

Therefore the measure of the vertex angle is .

The trick here is that we don't know which is the repeated side. Our possible triangles are therefore 20 + 20 + 30 = 70 or 30 + 30 + 20 = 80.  The difference is therefore 80 – 70 or 10.

Area of a triangle is ½ x base x height. Since base:height = 3:2, base = 1.5 height.  Area = 12 = ½ x 1.5 height x height or 24/1.5 = height².  Height = 4.  Base = 1.5 height = 6. Half the base and the height form the legs of a right triangle, with an equal leg of the isosceles triangle as the hypotenuse. This is a 3-4-5 right triangle.

This question is about the Triangle Inequality, which states that in a triangle with two sides A and B, the third side must be greater than the absolute value of the difference between A and B and smaller than the sum of A and B.

Applying the Triangle Inequality to this problem, we see that the third side must be greater than the absolute value of the difference between the other two sides, which is |6-6|=0, and smaller than the sum of the two other sides, which is 6+6=12. The only answer choice that does not satisfy this range of possible values is 12 since the third side must be LESS than 12.

An isoceles triangle is a triangle that has at least two congruent sides (and therefore, at least two congruent angles as well).

An isosceles triangle is basically two right triangles stuck together. The isosceles triangle has a base of 6, which means that from the midpoint of the base to one of the angles, the length is 3. Now, you have a right triangle with a base of 3 and a height of 4. The hypotenuse of this right triangle, which is one of the two congruent sides of the isosceles triangle, is 5 units long (according to the Pythagorean Theorem).

The total perimeter will be the length of the base (6) plus the length of the hypotenuse of each right triangle (5).

5 + 5 + 6 = 16

Drawing points gives sides of a right triangle of 4, 5, and an unknown hypotenuse.

Using the pythagorean theorem we find that the hypotenuse is .

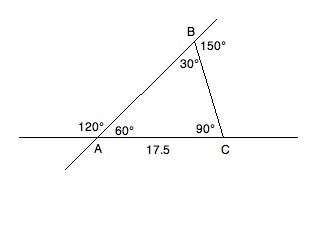
Consult the diagram above while reading the solution. Because of what we know about supplementary angles, we can fill in the inner values of the triangle. Angles A and B can be found by the following reductions:

A + 120 = 180; A = 60

B + 150 = 180; B = 30

Since we know A + B + C = 180 and have the values of A and B, we know:

60 + 30 + C = 180; C = 90

This gives us a 30:60:90 triangle. Now, since 17.5 is across from the 30° angle, we know that the other two sides will have to be √3 and 2 times 17.5; therefore, our perimeter will be as follows:

Because DC and AB are parallel, this means that angles CDB and ABD are equal. When two parallel lines are cut by a transversal line, alternate interior angles (such as CDB and ABD) are congruent.

Now, we can show that triangles ABD and BDC are similar. Both ABD and BDC are right triangles. This means that they have one angle that is the same—their right angle. Also, we just established that angles CDB and ABD are congruent. By the angle-angle similarity theorem, if two triangles have two angles that are congruent, they are similar. Thus triangles ABD and BDC are similar triangles.

We can use the similarity between triangles ABD and BDC to find the lengths of BC and CD. The length of BC is proportional to the length of AD, and the length of CD is proportional to the length of DB, because these sides correspond.

We don’t know the length of DB, but we can find it using the Pythagorean Theorem. Let a, b, and c represent the lengths of AD, AB, and BD respectively. According to the Pythagorean Theorem:

 a² + b² = c²

15² + 20² = c²

625 = c²

c = 25

The length of BD is 25.

We now have what we need to find the perimeter of the quadrilateral.

Perimeter = sum of the lengths of AB, BC, CD, and DA.

Perimeter = 20 + 18.75 + 31.25 + 15 = 85

The answer is 85.