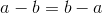For the product of three integers to be odd, all three integers must themselves be odd.

At least two of  must have the same odd/even status. The sum of those two numbers must be even, and since it is a factor of , then  itself must be even.

With many questions like this, it might be easier to plug in numbers rather than dealing with theoretical variables.  However, given that this question asks for the expression that is not always even or odd but only not necessarily odd, the theoretical route might be our only choice.

Therefore, our best approach is to simply analyze each answer choice.

:  Since  is odd,  is also odd, since and odd number multiplied by an odd number yields an odd product.  Since  is also odd, multiplying it by  will again yield an odd product, so this expression is always odd.

:  Since  is odd, multiplying it by 2 will yield an even number.  Subtracting this number from  will also give an odd result, since an odd number minus an even number gives an odd number.  Therefore, this answer is also always odd.

:  Since both numbers are odd, their product will also always be odd.

:  Since  is odd, multiplying it by 2 will give an even number.  Since  is odd, subtracting it from our even number will give an odd number, since an even number minus and odd number is always odd.  Therefore, this answer will always be odd.

:   Since both numbers are odd, there sum will be even.  However, dividing an even number by another even number (2 in our case) does not always produce an even or an odd number.  For example, 5 and 7 are both odd.  Their sum, 12, is even.  Dividing by 2 gives 6, an even number.  However, 5 and 9 are also both odd.  Their sum, 14, is even, but dividing by 2 gives 7, an odd number.  Therefore, this expression isn't necessarily always odd or always even, and is therefore our answer.

To find the answer to this question, calculate the total jelly beans for each person:

Portia:  * <Theodore's count of jelly beans>, which is  or 

Harvey:  * <Portia's count of jelly beans>, which is  or 

So, the total is:

(Do not forget that you need those original  for Theodore!)

An even number subtracted from an odd number will always produce an odd result.

None of the other answer choices are correct.

Pick any even integer (2, 4, 6, etc.) to represent x. The only value that is odd is 3x + 1. Any number multiplied by an even integer will be even. When an even number is added and subtracted to that product, the result will be even as well. 3x + 1 is the only choice that adds an odd number to the product.

While I & II can be true, examples can be found that show they are not always true (for example, 2²/2² is odd and 4²/2² is even).

III is always true – a square even number is always divisible by four, and the distributive property tell us that adding two numbers with a common factor gives a sum that also has that factor.

S consists of all even integers. If we were to increase each of these even numbers by 2, then we would get another set of even numbers, because adding 2 to an even number yields an even number. In other words, T also consists entirely of even numbers.

In order to find the mean of T, we would need to add up all of the elements in T and then divide by however many numbers are in T. If we were to add up all of the elements of T, we would get an even number, because adding even numbers always gives another even number. However, even though the sum of the elements in T must be even, if the number of elements in T was an even number, it's possible that dividing the sum by the number of elements of T would be an odd number.

For example, let's assume T consists of the numbers 2, 4, 6, and 8. If we were to add up all of the elements of T, we would get 20. We would then divide this by the number of elements in T, which in this case is 4. The mean of T would thus be 20/4 = 5, which is an odd number. Therefore, the mean of T doesn't have to be an even number.

Next, let's analyze the median of T. Again, let's pretend that T consists of an even number of integers. In this case, we would need to find the average of the middle two numbers, which means we would add the two numbers, which gives us an even number, and then we would divide by two, which is another even number. The average of two even numbers doesn't have to be an even number, because dividing an even number by an even number can produce an odd number.

For example, let's pretend T consists of the numbers 2, 4, 6, and 8. The median of T would thus be the average of 4 and 6. The average of 4 and 6 is (4+6)/2 = 5, which is an odd number. Therefore, the median of T doesn't have to be an even number.

Finally, let's examine the range of T. The range is the difference between the smallest and the largest numbers in T, which both must be even. If we subtract an even number from another even number, we will always get an even number. Thus, the range of T must be an even number.

Of choices I, II, and III, only III must be true.

The answer is III only.

I)xy is Even*Odd is Even. II) x-y is Even+/-Odd is Odd. III) 3x is Odd*Even =Even, 2y is Even*Odd=Even, Even + Even = Even. Therefore only II is Odd.

I. xyz = even * odd * even = even

II. 2x + 3y = even*even + odd*odd = even + odd = odd

III. z² – y = even * even – odd = even – odd = odd

Therefore only I will give an even number.

Since we are only told that "at least" one of the numbers is even, we could have one even and one odd integer OR we could have two even integers.

Even plus odd is odd, but even plus even is even, so x + y could be either even or odd.

Even times odd is even, and even times even is even, so xy must be even.