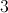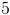In order to solve this problem, it will help us to find all of the possible scenarios of a, b, a², and b². We need to make use of the following rules:

1. The product of two even numbers is an even number.

2. The product of two odd numbers is an odd number.

3. The product of an even and an odd number is an even number.

The information that we are given is that ab² is an even number. Let's think of ab² as the product of two integers: a and b².

In order for the product of a and b² to be even, at least one of them must be even, according to the rules that we discussed above. Thus, the following scenarios are possible:

Scenario 1: a is even and b² is even

Scenario 2: a is even and b² is odd

Scenario 3: a is odd and b² is even

Next, let's consider what possible values are possible for b. If b² is even, then this means b must be even, because the product of two even numbers is even. If b were odd, then we would have the product of two odd numbers, which would mean that b² would be odd. Thus, if b² is even, then b must be even, and if b² is odd, then b must be odd. Let's add this information to the possible scenarios:

Scenario 1: a is even, b² is even, and b is even

Scenario 2: a is even, b² is odd, and b is odd

Scenario 3: a is odd, b² is even, and b is even

Lastly, let's see what is possible for a². If a is even, then a² must be even, and if a is odd, then a² must also be odd. We can add this information to the three possible scenarios:

Scenario 1: a is even, b² is even, and b is even, and a² is even

Scenario 2: a is even, b² is odd, and b is odd, and a² is even

Scenario 3: a is odd, b² is even, and b is even, and a² is odd

Now, we can use this information to examine choices I, II, and III.

Choice I asks us to determine if a² must be even. If we look at the third scenario, in which a is odd, we see that a² would also have to be odd. Thus it is possible for a² to be odd.

Next, we can analyze a²b. In the first scenario, we see that a² is even and b is even. This means that a²b would be even. In the second scenario, we see that a² is even, and b is odd, which would still mean that a²b is even. And in the third scenario, a² is odd and b is even, which also means that a²b would be even. In short, a²b is even in each of the possible scenarios, so it must always be even. Thus, choice II must be true. 

We can now look at ab. In scenario 1, a is even and b is even, which means that ab would also be even. In scenario 2, a is even and b is odd, which means that ab is even again. And in scenario 3, a is odd and b is even, which again means that ab is even. Therefore, ab must be even, and choice III must be true. 

The answer is II and III only.

The word "product" refers to the answer of a multiplication problem.  Since 2 times 8 equals 16, it is a valid pair of numbers.

If  is an odd integer then we can plug 1 into  and solve for  yielding 13. 13 is prime, meaning it is only divisible by 1 and itself.

Recall that when you multiply by an even number, you get an even product.

Therefore, we know the following from the first statement:

 is even or  is even or both  and  are even.

For the second, we know this:

Since  is even, therefore,  can be either even or odd. (Regardless of what it is, we can get an even value for .)  

Based on all this data, we can tell nothing necessarily about . If  is even, then  is even, even if  is odd. However, if  is odd while  is even, then  will be even.

In a group of philosophers,  are followers of Durandus. Twice that number are followers of Ockham. Four times the number of followers of Ockham are followers of Aquinas. One sixth of the number of followers of Aquinas are followers of Scotus. How many total philosophers are in the group?

To start, let's calculate the total philosophers:

Ockham:  * <Number following Durandus>, or 

Aquinas:  * <Number following Ockham>, or 

Scotus:  divided by , or 

Therefore, the total number is:

I is not always true because a negative number multiplied by 7 will give a number that is more negative than the original. II is true because adding 5 to any number will increase the value. III is true because squaring any number will increase the magnitude of the value, and squaring a negative number will make it positive.

There are certain patterns that can be used to predict whether the product or sum of numbers will be odd or even. The sum of two odd numbers is always even, as is the sum of two even numbers. The sum of an odd number and an even number is always odd. In multiplication the product of two odd numbers is always odd. While the product of even numbers, as well as the product of odd numbers multiplied by even numbers is always even. So for this problem we need to find scenarios where the only possibile answers are even.  can only result in even numbers no matter what positive integers are used for  and , because  must can only result in even products; the same can be said for . The rules provide that the sum of two even numbers is even, so  is the answer.

In order to find all of the numbers that are multiples of both 8 and 18, we need to find the least common mutliple (LCM) of 8 and 18. The easiest way to do this would be to list out the multiples of 8 and 18 and determine the smallest one that is common to both. 

First, let's list the first several multiples of eight:

8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88 . . .

Next, we list the first several multiples of eighteen:

18, 36, 54, 72, 90, 108, 126, 144 . . .

By comparing the multiples of eight and eighteen, we can see that the smallest one that they share is 72. Thus, the LCM of 8 and 18 is 72.

Because the LCM is 72, this means that every multiple of 72 is also a multiple of both 8 and 18. So, in order to find all of the multiples less than ten thousand that are both multiples of 8 and 18, we simply need to find how many multiples of 72 are less than 10000, and to do this, all we have to do is to divide 10000 by 72.

When we divide 10000 by 72, we get 138 with a remainder of 64; therefore, 72 will go into ten thousand 138 times before it exceeds ten thousand. In other words, there are 138 numbers less than 10000 that are multiples of 72 and, by extension, also multiples of both 8 and 18. 

The answer is 138.

The simplest way to solve this question is to go through each answer choice and check to see if it is divisible by 2, 4 and 7. When we do this, we find that only 168 is evenly divisible by each of these numbers. 114 is not divisible by 4 or 7, 172 is not divisibly by 7, 136 is not divisble by 7, and 154 is not divisible by 4.

We are told that a, b, and c are integers, and that 4a = 6b = 11c. Because a, b, and c are positive integers, this means that 4a represents all of the multiples of 4, 6b represents the multiples of 6, and 11c represents the multiples of 11. Essentially, we will need to find the least common multiples (LCM) of 4, 6, and 11, so that 4a, 6b, and 11c are all equal to one another.

First, let's find the LCM of 4 and 6. We can list the multiples of each, and determine the smallest multiple they have in common. The multiples of 4 and 6 are as follows:

4: 4, 8, 12, 16, 20, ...

6: 6, 12, 18, 24, 30, ...

The smallest multiple that 4 and 6 have in common is 12. Thus, the LCM of 4 and 6 is 12.

We must now find the LCM of 12 and 11, because we know that any multiple of 12 will also be a multiple of 4 and 6.

Let's list the first several multiples of 12 and 11:

12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, ...

11: 11, 22, 33, 44, 55, 66, 77, 88, 99, 110, 121, 132, ...

The LCM of 12 and 11 is 132.

Thus, the LCM of 4, 6, and 12 is 132.

Now, we need to find the values of a, b, and c, such that 4a = 6b = 12c = 132.

4a = 132

Divide each side by 4.

a = 33

Next, let 6b = 132.

6b = 132

Divide both sides by 6.

b = 22

Finally, let 11c = 132.

11c = 132

Divide both sides by 11.

c = 12.

Thus, a = 33, b = 22, and c = 12.

We are asked to find the value of a + b + c.

33 + 22 + 12 = 67.

The answer is 67.