All PSAT Math Resources
Example Questions
Example Question #4 : How To Find The Square Of An Integer
How many integers from 20 to 80, inclusive, are NOT the square of another integer?
First list all the integers between 20 and 80 that are squares of another integer:
52 = 25
62 = 36
72 = 49
82 = 64
In total, there are 61 integers from 20 to 80, inclusive. 61 – 4 = 57
Example Question #5 : How To Find The Square Of An Integer
Let the universal set be the set of all positive integers.
Let be the set of all multiples of 3; let be the set of all multiples of 7; let be the set of all perfect square integers. Which of the following statements is true of 243?
Note: means "the complement of ", etc.
, so 243 is divisible by 3. .
, so 243 is not divisible by 7. - that is, .
, 243 is not a perfect square integer. - that is, .
Since 243 is an element of , , and , it is an element of their intersection. The correct choice is that
Example Question #162 : Arithmetic
Consider the inequality:
Which of the following could be a value of ?
There is no possible value for
Notice how is the greatest value. This often means that is negative as when is odd and when is even.
Let us examine the first choice,
This can only be true of a negative value that lies between zero and one.
Example Question #202 : Arithmetic
In the equation above, if is a positive integer, what is the value of ?
Begin by squaring both sides of the equation:
Now solve for y:
Note that must be positive as defined in the original question. In this case, must be 12.
Example Question #2 : Factoring And Simplifying Square Roots
Simplify. Assume all variables are positive real numbers.
The index coefficent in is represented by . When no index is present, assume it is equal to 2. under the radical is known as the radican, the number you are taking a root of.
First look for a perfect square,
Then to your Variables
Take your exponents on both variables and determine the number of times our index will evenly go into both.
So you would take out a and would be left with a
*Dividing the radican exponent by the index - gives you the number of variables that should be pulled out.
The final answer would be .
Example Question #203 : Arithmetic
Simplify. Assume all integers are positive real numbers.
Index of means the cube root of Radican
Find a perfect cube in
Simplify the perfect cube, giving you .
Take your exponents on both variables and determine the number of times our index will evenly go into both.
The final answer would be
Example Question #3 : Factoring And Simplifying Square Roots
Simplify square roots. Assume all integers are positive real numbers.
Simplify as much as possible. List all possible answers.
1a.
1b.
1c.
and and
and and
and
and and
and and
When simplifying radicans (integers under the radical symbol), we first want to look for a perfect square. For example, is not a perfect square. You look to find factors of to see if there is a perfect square factor in , which there is.
1a.
Do the same thing for .
1b.
1c.Follow the same procedure except now you are looking for perfect cubes.
Example Question #1 : How To Simplify Square Roots
Simplify
9 ÷ √3
2
3
none of these
3√3
not possible
3√3
in order to simplify a square root on the bottom, multiply top and bottom by the root

Example Question #31 : Basic Squaring / Square Roots
Simplify:
√112
4√10
12
20
4√7
10√12
4√7
√112 = {√2 * √56} = {√2 * √2 * √28} = {2√28} = {2√4 * √7} = 4√7
Example Question #31 : Basic Squaring / Square Roots
Simplify:
√192
√192 = √2 X √96
√96 = √2 X √48
√48 = √4 X√12
√12 = √4 X √3
√192 = √(2X2X4X4) X √3
= √4X√4X√4 X √3
= 8√3
Certified Tutor
Certified Tutor
All PSAT Math Resources































































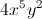
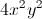


![\sqrt[n]{b}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/25860/gif.latex)









![\sqrt[3]{24x^{16}y^{12}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/25869/gif.latex)

![2x^{2}y^{3}\sqrt[3]{3xy}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/32046/gif.latex)
![2x^{5}y^{4}\sqrt[3]{3x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/32040/gif.latex)
![2x^{8}y^{4}\sqrt[3]{3x^{2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/32044/gif.latex)

![\sqrt[3]{24x^{16}y^{12}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/25870/gif.latex)




![\sqrt[3]{8\cdot 3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/25875/gif.latex)
![2\sqrt[3]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/25876/gif.latex)
![x\rightarrow \frac{16}{3}= 5^{\frac{1}{3}} \rightarrow x^{5}\sqrt[3]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/25877/gif.latex)

![2x^{5}y^{4}\sqrt[3]{3x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/25879/gif.latex)


![\sqrt[3]{24}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/25945/gif.latex)


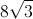


![2\sqrt[3]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/32084/gif.latex)

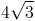
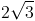
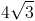
![2\sqrt[3]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/32078/gif.latex)






![\sqrt[3]{24}=\sqrt[3]{8\cdot 3}=\sqrt[3]{8}\cdot\sqrt[3]{3}=2\sqrt[3]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/25952/gif.latex)


