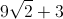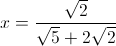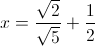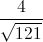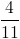Call Now to Set Up Tutoring:

(888) 888-0446

PSAT Math : Arithmetic

Study concepts, example questions & explanations for PSAT Math

Create An Account

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #11 : Basic Squaring / Square Roots

Mulitply and simplify. Assume all integers are positive real numbers.

$\sqrt{3}(3\sqrt{2}+\sqrt{3})$

Possible Answers:

$27\sqrt{2}$

$3\sqrt{6}+9$

$3\sqrt{6}+3$

$9\sqrt{2}+3$

$9\sqrt{6}$

Correct answer:

$3\sqrt{6}+3$

Explanation:

$\sqrt{3}(3\sqrt{2}+\sqrt{3})$

Order of operations, first distributing the $\sqrt{3}$ to all terms inside the parentheses.

$(1\cdot 3\sqrt{3}\cdot \sqrt{2})+(\sqrt{3}\cdot\sqrt{3})$

$3\sqrt{3\cdot 2}+\sqrt{3\cdot 3}\rightarrow3\sqrt{6}+\sqrt{9}\rightarrow3\sqrt{6}+3$

The final answer is $3\sqrt{6}+3$ .

Report an Error

Example Question #1 : How To Multiply Square Roots

The square root(s) of 36 is/are ________.

Possible Answers:

-6

6 and -6

None of these answers are correct.

6, -6, and 0

Correct answer:

6 and -6

Explanation:

To square a number is to multiply that number by itself. Because 6 x 6 = 36 AND -6 x -6 = 36, both 6 and -6 are square roots of 36.

Report an Error

Example Question #1 : How To Multiply Square Roots

Simplify:

$\sqrt{4}*\sqrt{12}*\sqrt{5}$

Possible Answers:

$\sqrt{15}$

$\sqrt{21}$

$4\sqrt{15}$

$5\sqrt{12}$

$2\sqrt{60}$

Correct answer:

$4\sqrt{15}$

Explanation:

Multiplication of square roots is easy! You just have to multiply their contents by each other. Just don't forget to put the result "under" a square root! Therefore:

$\sqrt{4}*\sqrt{12}*\sqrt{5}$

becomes

$\sqrt{4*12*5}=\sqrt{240}$

Now, you need to simplify this:

$\sqrt{240} = \sqrt{2*2*2*2*3*5}$

You can "pull out" two s. (Note, that it would be even easier to do this problem if you factor immediately instead of finding out that 4*12*5 = 240 .)

After pulling out the s, you get:

$\sqrt{2*2*2*2*3*5} = 2*2(\sqrt{3*5}) = 4\sqrt{15}$

Report an Error

Example Question #191 : Arithmetic

Solve for $\dpi{100} x$ :

$x\sqrt{45}+x\sqrt{72}=\sqrt{18}$

Possible Answers:

$x=\sqrt{9}$

$x=3$

$x=\frac{\sqrt{2}}{\sqrt{5}}+\frac{1}{2}$

$x=\frac{\sqrt{5}}{\sqrt{2}}+2$

$x=\frac{\sqrt{2}}{\sqrt{5}+2\sqrt{2}}$

Correct answer:

$x=\frac{\sqrt{2}}{\sqrt{5}+2\sqrt{2}}$

Explanation:

$x\sqrt{45}+x\sqrt{72}=\sqrt{18}$

Notice how all of the quantities in square roots are divisible by 9

$x\sqrt{9\times 5}+x\sqrt{9\times 8}=\sqrt{9\times 2}$

$x\sqrt{9}\sqrt{5}+x\sqrt{9}\sqrt{4\times 2}=\sqrt{9}\sqrt{2}$

$3x\sqrt{5}+3x\sqrt{4}\sqrt{2}=3\sqrt{2}$

$3x\sqrt{5}+6x\sqrt{2}=3\sqrt{2}$

$x(3\sqrt{5}+6\sqrt{2})=3\sqrt{2}$

$x=\frac{3\sqrt{2}}{3\sqrt{5}+6\sqrt{2}}$

Simplifying, this becomes

$x=\frac{\sqrt{2}}{\sqrt{5}+2\sqrt{2}}$

Report an Error

Example Question #192 : Arithmetic

If m and n are postive integers and 4^m = 2ⁿ, what is the value of m/n?

Possible Answers:

1/2

Correct answer:

1/2

Explanation:

2²= 4. Also, following the rules of exponents, 4¹= 1.
One can therefore say that m = 1 and n = 2.
The question asks to solve for m/n. Since m = 1 and n = 2, m/n = 1/2.

Report an Error

Example Question #193 : Arithmetic

Simplify the radical:

$\sqrt{320}$

Possible Answers:

$8\sqrt{20}$

$4\sqrt{5}$

$8\sqrt{5}$

$\sqrt{320}$

$4\sqrt{20}$

Correct answer:

$8\sqrt{5}$

Explanation:

$\sqrt{320}=\sqrt{2\times 160}=\sqrt{2\times 2\times 80}=2\sqrt{80}=2\sqrt{2\times 40}=2\sqrt{2\times 2\times 20}=2\times 2\times \sqrt{20}=4\sqrt{2\times 10}=4\sqrt{2\times 2\times 5}=4\times 2\times \sqrt{5}=8\sqrt{5}$

Report an Error

Example Question #194 : Arithmetic

Simplify.

$\sqrt{\frac{16}{121}}$

Possible Answers:

$\frac{16}{121}$

$\frac{4}{\sqrt{121}}$

$\frac{8}{61}$

$16\sqrt{121}$

$\frac{4}{11}$

Correct answer:

$\frac{4}{11}$

Explanation:

$\sqrt{\frac{16}{121}}$

Take the square root of both the top and bottom terms.

$\frac{\sqrt{16}}{\sqrt{121}}$

Simplify.

$\frac{4}{11}$

Report an Error

Example Question #2 : How To Find The Square Of An Integer

The square root of 5184 is:

Possible Answers:

Correct answer:

Explanation:

The easiest way to narrow down a square root from a list is to look at the last number on the squared number – in this case 4 – and compare it to the last number of the answer.

70 * 70 will equal XXX0

71 * 71 will equal XXX1

72 * 72 will equal XXX4

73 * 73 will equal XXX9

74 * 74 will equal XXX(1)6

Therefore 72 is the answer. Check by multiplying it out.

Report an Error

Example Question #195 : Arithmetic

If $5^{x}+5^{x}+5^{x}+5^{x}+5^{x}=5^{10}$ , what is the value of x?

Possible Answers:

Correct answer:

Explanation:

$5(5^{x})=5^{10}$

$5^{1}(5^{x})=5^{10}$

$5^{x+1}=5^{10}$

$x=9$

Report an Error

Example Question #1 : How To Find The Square Of An Integer

If x and y are integers and xy + y² is even, which of the following statements must be true?

I. 3y is odd

II. y/2 is an integer

III. x^y is even

Possible Answers:

II only

I & II

I only

I, II, & III

$None\ of\ the\ statements\ must\ be\ true$

Correct answer:

$None\ of\ the\ statements\ must\ be\ true$

Explanation:

In order for the original statement to be true, the and $y^{2}$ terms must be either both odd or both even. Looking at each of the statements individually,

I. States that is odd, but only odd values multiplied by 3 are odd. If was an even number, the result would be even. But can be either odd or even, depending on what equals. Thus this statement COULD be true but does not HAVE to be true.

II. States that $\frac{y}{2}$ is an integer, and since only even numbers are cleanly divided by 2 (odd values result in a fraction) this ensures that is even. However, can also be odd, so this is a statement that COULD be true but does not HAVE to be true.

III. For exponents, only the base value determines whether it is even or odd - it does not indicate the value of y at all. Only even numbers raised to any power are even, thus, this ensures that is even. But can be odd as well, so this statement COULD be true but does not HAVE to be true.

An example of two integers that will work violate conditions II and III is x=1 and y=3 .

$(1)\cdot (3)+(3)^{2}=3+9=12$ , and even number.

$\frac{3}{2}$ is not an integer.

$1^{3}=1$ is not even.

Furthermore, any combination of 2 even integers will make the original statement true, and violate the Statement I.

Report an Error

View PSAT Mathematics Tutors

Eva
Certified Tutor

Technicka Univerzita Liberec, Bachelor of Education, Education.

View PSAT Mathematics Tutors

Kelly
Certified Tutor

Rhode Island College, Bachelors, History/Political Science. Rhode Island College, Masters, History.

View PSAT Mathematics Tutors

Keith
Certified Tutor

Xavier University, Bachelor in Business Administration, Accounting. Ohio University-Main Campus, Masters in Education, Mathem...

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in New York City, SAT Tutors in Philadelphia, Physics Tutors in Boston, ACT Tutors in Los Angeles, GMAT Tutors in Houston, MCAT Tutors in Philadelphia, Chemistry Tutors in San Francisco-Bay Area, GMAT Tutors in Denver, Computer Science Tutors in Phoenix, Calculus Tutors in Denver

Popular Courses & Classes

LSAT Courses & Classes in Houston, GRE Courses & Classes in New York City, GRE Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Houston, ISEE Courses & Classes in Atlanta, SSAT Courses & Classes in Washington DC, GRE Courses & Classes in Boston, GRE Courses & Classes in Houston, Spanish Courses & Classes in Washington DC, MCAT Courses & Classes in Denver

Popular Test Prep

ISEE Test Prep in Washington DC, GMAT Test Prep in New York City, ACT Test Prep in Miami, LSAT Test Prep in Philadelphia, MCAT Test Prep in Los Angeles, SAT Test Prep in Denver, SAT Test Prep in Seattle, GRE Test Prep in Denver, MCAT Test Prep in Miami, GRE Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

PSAT Math : Arithmetic

Study concepts, example questions & explanations for PSAT Math

All PSAT Math Resources

Example Questions

Example Question #11 : Basic Squaring / Square Roots

Example Question #1 : How To Multiply Square Roots

Example Question #1 : How To Multiply Square Roots

Example Question #191 : Arithmetic

Example Question #192 : Arithmetic

Example Question #193 : Arithmetic

Example Question #194 : Arithmetic

Example Question #2 : How To Find The Square Of An Integer

Example Question #195 : Arithmetic

Example Question #1 : How To Find The Square Of An Integer

All PSAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: