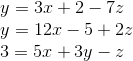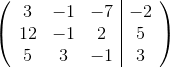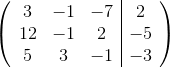Call Now to Set Up Tutoring:

(888) 888-0446

Precalculus : Pre-Calculus

Study concepts, example questions & explanations for Precalculus

Create An Account

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #31 : Multiplication Of Matrices

Multiply the matrices: $\begin{bmatrix} 1& 3 \end{bmatrix}\begin{bmatrix} 4&9 \end{bmatrix}$

Possible Answers:

$\begin{bmatrix} 5& 12 \end{bmatrix}$

$\textup{Cannot be solved.}$

$\begin{bmatrix} 4& 27 \end{bmatrix}$

108

Correct answer:

$\textup{Cannot be solved.}$

Explanation:

In order to multiply these matrices we will need to consider the rows and columns for each matrix.

Both matrices have a dimension of $1\times 2$ .

The rule for multiplying matrices is where the number of columns of the first matrix must match the number of rows of the second matrix.

If the dimensions of the first matrix are $a\times b$ , and the dimensions of the second matrix are $b\times c$ , then we will get a dimension of $a \times c$ matrix as a result. If the value of are not matched, we cannot evaluate the product of the matrices.

The correct answer is: $\textup{Cannot be solved.}$

Report an Error

Example Question #61 : Matrices And Vectors

Find the product of A and B.

$A=\begin{bmatrix} 3 &-1 &4 \end{bmatrix}$

$B=\begin{bmatrix} 2\\ 1\\-3 \end{bmatrix}$

Possible Answers:

$\begin{bmatrix} -7 \end{bmatrix}$

$\begin{bmatrix} 6 & -2& -1\\4 &3 &-6 \\2 &5 &6 \end{bmatrix}$

$\begin{bmatrix} 1 \end{bmatrix}$

$\begin{bmatrix} 6 &-1 &-12 \end{bmatrix}$

Correct answer:

$\begin{bmatrix} -7 \end{bmatrix}$

Explanation:

Since you are multiplying a $1\times 3$ to a $3\times 1$ , the answer is going to be a $1\times 1$ .

To solve, simply multiply each corresponding element and add together.

Thus, your answer is

[-7] .

Report an Error

Example Question #581 : Pre Calculus

What is the inverse of the following nxn matrix

$\begin{bmatrix} 1 & 0 &0 &0 &1 \\ 1& 0&0 &0 & 1\\ \vdots &\vdots& \vdots &\vdots & \vdots\\ 1 &0 &0 & 0 &1 \\ 1 & 0 &0 &0 &1 \end{bmatrix}$

Possible Answers:

The matrix is not invertible.

(-1)^n

Correct answer:

The matrix is not invertible.

Explanation:

Note the first and the last columns are equal.

Therefore, when we try to find the determinant using the following formula we get the determinant equaling 0:

$\begin{bmatrix} 1 & 0 & 1\\1 & 0 & 1\\1 & 0 & 1\end{bmatrix}=1\begin{bmatrix}0 &1\\0&1 \end{bmatrix}-0\begin{bmatrix}1 & 1\\1 &1 \end{bmatrix}+1\begin{bmatrix} 1 &0\\1&0\end{bmatrix}$

=1(0-0)-0(1-1)+1(0-0)

=0+0+0

This means simply, that the matrix does not have an inverse.

Report an Error

Example Question #1 : Find The Multiplicative Inverse Of A Matrix

Find the inverse of the matrix

$\begin{pmatrix} 1&2 \\ 2&4 \end{pmatrix}$ .

Possible Answers:

$\begin{pmatrix} 0.5&1 \\ 1&2 \end{pmatrix}$

Does not exist

$\begin{pmatrix} 4&-2 \\ -2&1 \end{pmatrix}$

$\begin{pmatrix} 2&4 \\ 1&2 \end{pmatrix}$

Correct answer:

Does not exist

Explanation:

For a 2x2 matrix

$\begin{pmatrix} a&b \\ c&d \end{pmatrix}$

the inverse can be found by

$\frac{1}{det(A)}\begin{pmatrix} d&-b \\ -c&a \end{pmatrix}$

Because the determinant is equal to zero in this problem, or

$1\cdot4-2\cdot2=4-4=0$ ,

the inverse does not exist.

Report an Error

Example Question #2 : Find The Multiplicative Inverse Of A Matrix

Find the inverse of the matrix.

$A=\begin{pmatrix} 6& 2\\ 1& 5 \end{pmatrix}$

Possible Answers:

$A^{-1}=\begin{pmatrix} \frac{3}{14}&\frac{1}{14} \\ \\ \frac{1}{28}&\frac{5}{28} \end{pmatrix}$

$A^{-1}=\begin{pmatrix} \frac{3}{14}&\frac{-1}{14} \\ \\ \frac{-1}{28}&\frac{5}{28} \end{pmatrix}$

$A^{-1}=\begin{pmatrix} \frac{5}{28}&\frac{-1}{14} \\ \\ \frac{-1}{28}& \frac{3}{14} \end{pmatrix}$

$A^{-1}=\begin{pmatrix} 5&-2 \\ -1&6 \end{pmatrix}$

Correct answer:

$A^{-1}=\begin{pmatrix} \frac{5}{28}&\frac{-1}{14} \\ \\ \frac{-1}{28}& \frac{3}{14} \end{pmatrix}$

Explanation:

We use the inverse of a 2x2 matrix formula to determine the answer. Given a matrix

$A=\begin{pmatrix} a&b \\ c& d \end{pmatrix}$ it's inverse is given by the formula:

$A^{-1}=\frac{1}{\det A}\begin{pmatrix} d&-b \\ -c&a \end{pmatrix}$

First we define the determinant of our matrix:

$\det A=ad-bc=6\cdot5-2\cdot1=30-2=28$

Then,

$A^{-1}=\frac{1}{28}\begin{pmatrix} 5&-2 \\ -1& 6 \end{pmatrix}=\begin{pmatrix} \frac{5}{28}&\frac{-1}{14} \\ \\ \frac{-1}{28}&\frac{3}{14} \end{pmatrix}$

Report an Error

Example Question #1 : Find The Multiplicative Inverse Of A Matrix

Find the inverse of the following matrix.

$\begin{bmatrix} 1&\pi \\ \pi & \pi^2 \end{bmatrix}$

Possible Answers:

$\begin{bmatrix}1 & 0\\0&0 \end{bmatrix}$

$\begin{bmatrix} 1+\pi &\sqrt{\pi} \\ -\pi^2 & \pi^2-\pi \end{bmatrix}$

$\begin{bmatrix} 1&\pi \\ -\pi & \pi^2 \end{bmatrix}$

$\begin{bmatrix} 1&\sqrt{\pi} \\ \pi & \pi^2 \end{bmatrix}$

This matrix has no inverse.

Correct answer:

This matrix has no inverse.

Explanation:

This matrix has no inverse because the columns are not linearly independent. This means if you row reduce to try to compute the inverse, one of the rows will have only zeros, which means there is no inverse.

Report an Error

Example Question #1 : Find The Multiplicative Inverse Of A Matrix

Find the multiplicative inverse of the following matrix:

$\begin{bmatrix} 2&3 \\ 1&1 \end{bmatrix}$

Possible Answers:

$\begin{bmatrix} -1&3 \\ 1&-2 \end{bmatrix}$

$\begin{bmatrix} 1&1 \\ 3& 2 \end{bmatrix}$

This matrix has no inverse.

$\begin{bmatrix} \frac{1}{2}&\frac{1}{3} \\ 1& 1 \end{bmatrix}$

$\begin{bmatrix} -2&-3 \\ -1&-1 \end{bmatrix}$

Correct answer:

$\begin{bmatrix} -1&3 \\ 1&-2 \end{bmatrix}$

Explanation:

By writing the augmented matrix $\begin{bmatrix} 2& 3&| 1 &0 \\ 1& 1& |0&1 \end{bmatrix}$ , and reducing the left side to the identity matrix, we can implement the same operations onto the right side, and we arrive at $\begin{bmatrix} 1&0 |& -1& 3\\ 0& 1|& 1& -2 \end{bmatrix}$ , with the right side representing the inverse of the original matrix.

Report an Error

Example Question #1 : Find The Multiplicative Inverse Of A Matrix

Find the inverse of the matrix

$A = \begin{pmatrix} 2 & -1 \\ 1 & -5 \end{pmatrix}$

Possible Answers:

$\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$

None of the other answers.

$\begin{pmatrix} 5 & -1 \\ 1 & -2 \end{pmatrix}$

$\begin{pmatrix} \frac{5}{9} & -\frac{1}{9} \\ \frac{1}{9} & -\frac{2}{9} \end{pmatrix}$

$\begin{pmatrix} \frac{5}{9} & \frac{1}{9} \\ \frac{1}{9} & \frac{2}{9} \end{pmatrix}$

Correct answer:

$\begin{pmatrix} \frac{5}{9} & -\frac{1}{9} \\ \frac{1}{9} & -\frac{2}{9} \end{pmatrix}$

Explanation:

There are a couple of ways to do this. I will use the determinant method.

First we need to find the determinant of this matrix, which is

ad-bc

for a matrix in the form:

$\begin{pmatrix} a & b \\ c & d \end{pmatrix}$ .

Substituting in our values we find the determinant to be:

(2)(-5)-(-1)(1) = -9

Now one formula for finding the inverse of the matrix is

$\frac{1}{det[A]}adj[A]=\frac{1}{ad-bc}\begin{pmatrix} d& -b\\ -c&a \end{pmatrix}$

$= \frac{1}{-9}\begin{pmatrix} -5 &1 \\ -1 & 2 \end{pmatrix}$

$= \begin{pmatrix} \frac{5}{9} & -\frac{1}{9} \\ \frac{1}{9} & -\frac{2}{9} \end{pmatrix}$ .

Report an Error

Example Question #582 : Pre Calculus

What is the inverse of the identiy matrix $\begin{bmatrix} 1& 0\\ 0 &1 \end{bmatrix}$ ?

Possible Answers:

The identity matrix $\begin{bmatrix} 1&0 \\0 & 1 \end{bmatrix}$

$\begin{bmatrix} 1& 1\\ 1 & 1 \end{bmatrix}$

$\begin{bmatrix} 2& -1\\-1 & 2 \end{bmatrix}$

$\begin{bmatrix} 0&0 \\0 & 0 \end{bmatrix}$

Correct answer:

The identity matrix $\begin{bmatrix} 1&0 \\0 & 1 \end{bmatrix}$

Explanation:

By definition, an inverse matrix is the matrix B that you would need to multiply matrix A by to get the identity. Since the identity matrix yields whatever matrix it is being multiplied by, the answer is the identity itself.

Report an Error

Example Question #1 : Solve A System Of Equations In Three Variables Using Augmented Matrices

Express this system of equations as an augmented matrix:

$\\y=3x+2-7z\\ y=12x-5+2z\\ 3=5x+3y-z$

Possible Answers:

$\left(\begin{array}{ccc|c} 3 & 2 & -7 & 1\\ 12 & -5 & 2 & 1 \\ 5 & 3 & -1 & 3 \end{array}\right)$

$\left(\begin{array}{ccc|c} 3 & -1 & -7 & -2\\ 12 & -1 & 2 & 5\\ 5 & 3 & -1 & 3 \end{array}\right)$

$\left(\begin{array}{ccc|c} 3 & -1 & -7 & -2\\ 12 & -1 & 2 & 5 \end{array}\right)$

$\left(\begin{array}{ccc|c} 3 & -7 & 2 & 1\\ 12 & 2 & -5 & 1\\ 5 & -1 & -3 & 3 \end{array}\right)$

$\left(\begin{array}{ccc|c} 3 & -1 & -7 & 2\\ 12 & -1 & 2 & -5\\ 5 & 3 & -1 & -3 \end{array}\right)$

Correct answer:

$\left(\begin{array}{ccc|c} 3 & -1 & -7 & -2\\ 12 & -1 & 2 & 5\\ 5 & 3 & -1 & 3 \end{array}\right)$

Explanation:

Arrange the equations into the form:

ax+by+cz=d , where a,b,c,d are constants.

Then we have the system of equations: $\begin{align*} 3x-y-7z&=-2 \\ 12x-y+2z&=5 \\ 5x+3y-z&=3 \end{align*}$ .

The augmented matrix is found by copying the constants into the respective rows and columns of a matrix.

The vertical line in the matrix is analogous to the = sign thus resulting in the following:

$\left(\begin{array}{ccc|c} 3 & -1 & -7 & -2\\ 12 & -1 & 2 & 5\\ 5 & 3 & -1 & 3 \end{array}\right)$

Report an Error

View Pre-Calculus Tutors

James
Certified Tutor

St. Mary of the Plains College, Bachelors, Mathematics. Baker University, Masters, Business Administration and Management.

View Pre-Calculus Tutors

Tom
Certified Tutor

University of Wisconsin-Madison, Bachelor of Science, Atmospheric Sciences and Meteorology. Embry-Riddle Aeronautical Univers...

View Pre-Calculus Tutors

Mohammed
Certified Tutor

University of Maryland-College Park, Bachelor of Science, Electrical Engineering. University of Maryland-College Park, Master...

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Denver, ISEE Tutors in Boston, LSAT Tutors in Los Angeles, Statistics Tutors in New York City, Reading Tutors in Los Angeles, MCAT Tutors in Chicago, GRE Tutors in Chicago, Biology Tutors in Denver, Spanish Tutors in Miami, Calculus Tutors in Dallas Fort Worth

Popular Courses & Classes

MCAT Courses & Classes in Philadelphia, GRE Courses & Classes in Miami, Spanish Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Los Angeles, ISEE Courses & Classes in Miami, MCAT Courses & Classes in Chicago, GRE Courses & Classes in Phoenix, ACT Courses & Classes in Miami, Spanish Courses & Classes in Washington DC, SSAT Courses & Classes in Miami

Popular Test Prep

ISEE Test Prep in Miami, LSAT Test Prep in Miami, GMAT Test Prep in Atlanta, LSAT Test Prep in Houston, MCAT Test Prep in New York City, SSAT Test Prep in San Diego, SAT Test Prep in Philadelphia, SAT Test Prep in Boston, GRE Test Prep in Phoenix, ACT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Precalculus : Pre-Calculus

Study concepts, example questions & explanations for Precalculus

All Precalculus Resources

Example Questions

Example Question #31 : Multiplication Of Matrices

Example Question #61 : Matrices And Vectors

Example Question #581 : Pre Calculus

Example Question #1 : Find The Multiplicative Inverse Of A Matrix

Example Question #2 : Find The Multiplicative Inverse Of A Matrix

Example Question #1 : Find The Multiplicative Inverse Of A Matrix

Example Question #1 : Find The Multiplicative Inverse Of A Matrix

Example Question #1 : Find The Multiplicative Inverse Of A Matrix

Example Question #582 : Pre Calculus

Example Question #1 : Solve A System Of Equations In Three Variables Using Augmented Matrices

All Precalculus Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: