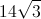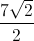We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Precalculus : Graphs and Inverses of Trigonometric Functions

Study concepts, example questions & explanations for Precalculus

Create An Account

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Graphs And Inverses Of Trigonometric Functions

Triangle

What is the $\sin C$ ?

Possible Answers:

$\frac{AB}{BC}$

$\frac{AC}{AB}$

$\frac{BC}{AB}$

$\frac{AB}{AC}$

$\frac{BC}{AC}$

Correct answer:

$\frac{AB}{AC}$

Explanation:

$\sin X = \frac{OPPOSITE}{HYPOTENUSE}$

$\sin C = \frac{AB}{AC}$

Report an Error

Example Question #2 : Graphs And Inverses Of Trigonometric Functions

Triangle

In the right triangle above, which of the following expressions gives the length of y?

Possible Answers:

$x\sin\theta$

$x\cos\theta$

$\frac{\sin(x)}{\theta}$

$x\tan\theta$

$\cos(x\times \theta)$

Correct answer:

$x\cos\theta$

Explanation:

$\cos\theta$ is defined as the ratio of the adjacent side to the hypotenuse, or in this case $\frac{y}{x}$ . Solving for y gives the correct expression.

Report an Error

Example Question #1 : Arcsin, Arccos, Arctan

Trig_id

What is $\theta$ if o=10 and a=8 ?

Possible Answers:

$53.14^{\circ}$

$89.60^{\circ}$

$0.90^{\circ}$

$55.14^{\circ}$

$51.34^{\circ}$

Correct answer:

$51.34^{\circ}$

Explanation:

In order to find $\theta$ we need to utilize the given information in the problem. We are given the opposite and adjacent sides. We can then, by definition, find the $\tan$ of $\theta$ and its measure in degrees by utilizing the $\arctan$ function.

$\tan=\frac{opposite}{adjacent}$

$\tan=\frac{10}{8}$

$\tan=1.25$

Now to find the measure of the angle using the $\arctan$ function.

$\theta=\arctan1.25$

$\rightarrow 51.34^{\circ}$

If you calculated the angle's measure to be $0.90^{\circ}}$ then your calculator was set to radians and needs to be set on degrees.

Report an Error

Example Question #1 : Graphs And Inverses Of Trigonometric Functions

Trig_id

If $\theta$ equals $55^{\circ}$ and is 15ft , how long is ?

Possible Answers:

12.3ft

13.2ft

8.6ft

Not enough information to solve

11.3ft

Correct answer:

12.3ft

Explanation:

This problem can be easily solved using trig identities. We are given the hypotenuse (15ft) and $\theta (55^{\circ})$ . We can then calculate side using the $\sin$ .

$\sin=\frac{opposite}{hypotenuse}$

$\sin55^{\circ}=\frac{o}{15ft}$

Rearrange to solve for .

$o=\sin55^{\circ}*15ft$

$\dpi{100} \rightarrow 12.3ft$

If you calculated the side to equal 8.6ft then you utilized the $\cos$ function rather than the $\sin$ .

Report an Error

Example Question #2 : Graphs And Inverses Of Trigonometric Functions

Triangle

What is the length of CB?

Possible Answers:

$\frac{AB}{\tan C}$

$\frac{\tan C}{AB}$

$\frac{AB}{\sin A}$

$\frac{AC}{\sin A}$

$\frac{\sin B}{AC}$

Correct answer:

$\frac{AB}{\tan C}$

Explanation:

$\tan X= \frac{OPPOSITE}{ADJACENT}$

$\tan C=\frac{AB}{CB}$

$CB= \frac{AB}{\tan C}$

Report an Error

Example Question #3 : Graphs And Inverses Of Trigonometric Functions

Rt_triangle_letters

In this figure, angle $a=30^\circ$ . If side Z =12 and Y=20 , what is the value of angle ?

Possible Answers:

$0.83^\circ$

$24^\circ$

Undefined

$90^\circ$

$56.44^\circ$

Correct answer:

$56.44^\circ$

Explanation:

For this problem, use the law of sines:

$\frac{\text{side opposite }a}{\sin(a)}=\frac{\text{side opposite }b}{\sin(b)}=\frac{\text{side opposite }c}{\sin(c)}$ .

In this case, we have values that we can plug in:

$\frac{\text{side opposite }a}{\sin(a)}=\frac{\text{side opposite }b}{\sin(b)}$

$\frac{Z}{\sin(a)}=\frac{Y}{\sin{(b)}}$

$\frac{12}{\sin(30^\circ)}=\frac{20}{\sin{(b)}}$

$24=\frac{20}{\sin(b)}$

$\sin(b)=\frac{20}{24}$

$b=\sin^{-1}(\frac{20}{24})$

$b=56.44^\circ$

Report an Error

Example Question #1 : Graphing The Sine And Cosine Functions

Rt_triangle_letters In this figure, if angle $a=18.5^\circ$ , side Z =30.2 , and side Y=17.2 , what is the value of angle ?

(NOTE: Figure not necessarily drawn to scale.)

Possible Answers:

$61.22^\circ$

$10.41^\circ$

$33.6^\circ$

$71.5^\circ$

Undefined

Correct answer:

$10.41^\circ$

Explanation:

First, observe that this figure is clearly not drawn to scale. Now, we can solve using the law of sines:

$\frac{\text{side opposite }a}{\sin(a)}=\frac{\text{side opposite }b}{\sin(b)}=\frac{\text{side opposite }c}{\sin(c)}$ .

In this case, we have values that we can plug in:

$\frac{\text{side opposite }a}{\sin(a)}=\frac{\text{side opposite }b}{\sin(b)}$

$\frac{Z}{\sin(a)}=\frac{Y}{\sin{(b)}}$

$\frac{30.2}{\sin(18.5^\circ)}=\frac{17.2}{\sin{(b)}}$

$95.18=\frac{17.2}{\sin(b)}$

$\sin(b)=\frac{17.2}{95.18}$

$b=\sin^{-1}(\frac{17.2}{95.18})$

$b=10.41^\circ$

Report an Error

Example Question #2 : Graphing The Sine And Cosine Functions

Rt_triangle_letters

In this figure, if angle $c=90^\circ$ , side X=12 , and side Z=8 , what is the measure of angle ?

Possible Answers:

Undefined

$90^\circ$

$48.2^\circ$

$41.8^\circ$

$\frac{2}{3}^\circ$

Correct answer:

$41.8^\circ$

Explanation:

Since $c=90^\circ$ , we know we are working with a right triangle.

That means that $\sin(\theta)=\frac{\text{opposite}}{\text{hypotenuse}}$ .

In this problem, that would be:

$\sin(a)=\frac{\text{Z}}{\text{X}}$

Plug in our given values:

$\sin(a)=\frac{8}{12}$

$\sin(a)=\frac{2}{3}$

$a=\sin^{-1}(\frac{2}{3})$

$a=41.8^\circ$

Report an Error

Example Question #1 : Understanding 30 60 90 Triangles

Rt_triangle_letters

In this figure, X=12 , $Y=6\sqrt{3}$ , and Z=6 . What is the value of angle ?

Possible Answers:

Undefined

$45^\circ$

$90^\circ$

$30^\circ$

$60^\circ$

Correct answer:

$30^\circ$

Explanation:

Notice that these sides fit the pattern of a 30:60:90 right triangle: $x:x\sqrt{3}:2x$ .

In this case, x=6 .

Since angle is opposite , it must be $30^\circ$ .

Report an Error

Example Question #2 : Understanding 30 60 90 Triangles

A triangle has angles of $30^\circ:60^\circ:90^\circ$ . If the side opposite the $30^\circ$ angle is , what is the length of the side opposite $60^\circ$ ?

Possible Answers:

$7\sqrt{2}$

$7\sqrt{3}$

$\frac{7\sqrt{2}}{2}$

$14\sqrt{3}$

Correct answer:

$7\sqrt{3}$

Explanation:

The pattern for $30^\circ:60^\circ:90^\circ$ is that the sides will be $x:x\sqrt{3}:2x$ .

If the side opposite $30^\circ$ is , then the side opposite $60^\circ$ will be $7\sqrt{3}$ .

Report an Error

View Pre-Calculus Tutors

James
Certified Tutor

University of Georgia, Bachelor in Arts, Political Science and Government.

View Pre-Calculus Tutors

Steven
Certified Tutor

Georgia Institute of Technology-Main Campus, Bachelor of Engineering, Industrial Engineering.

View Pre-Calculus Tutors

MEER
Certified Tutor

IIT , Master's/Graduate, Microelectronics .

All Precalculus Resources

12 Diagnostic Tests 380 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Reading Tutors in Atlanta, Statistics Tutors in New York City, Computer Science Tutors in Los Angeles, LSAT Tutors in San Francisco-Bay Area, Math Tutors in New York City, Spanish Tutors in Los Angeles, Chemistry Tutors in Dallas Fort Worth, MCAT Tutors in Seattle, SAT Tutors in Philadelphia, English Tutors in Philadelphia

Popular Courses & Classes

GMAT Courses & Classes in Washington DC, SSAT Courses & Classes in Los Angeles, GMAT Courses & Classes in Boston, Spanish Courses & Classes in San Diego, SSAT Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in Los Angeles, ACT Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Washington DC, GRE Courses & Classes in Boston, SAT Courses & Classes in Chicago

Popular Test Prep

GMAT Test Prep in Washington DC, SAT Test Prep in Los Angeles, GMAT Test Prep in Los Angeles, SAT Test Prep in Denver, SSAT Test Prep in Philadelphia, SAT Test Prep in New York City, ISEE Test Prep in New York City, ACT Test Prep in Miami, MCAT Test Prep in San Diego, MCAT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Precalculus : Graphs and Inverses of Trigonometric Functions

Study concepts, example questions & explanations for Precalculus

All Precalculus Resources

Example Questions

Example Question #1 : Graphs And Inverses Of Trigonometric Functions

Example Question #2 : Graphs And Inverses Of Trigonometric Functions

Example Question #1 : Arcsin, Arccos, Arctan

Example Question #1 : Graphs And Inverses Of Trigonometric Functions

Example Question #2 : Graphs And Inverses Of Trigonometric Functions

Example Question #3 : Graphs And Inverses Of Trigonometric Functions

Example Question #1 : Graphing The Sine And Cosine Functions

Example Question #2 : Graphing The Sine And Cosine Functions

Example Question #1 : Understanding 30 60 90 Triangles

Example Question #2 : Understanding 30 60 90 Triangles

All Precalculus Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: