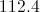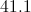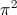Precalculus : Graphs and Inverses of Trigonometric Functions
Study concepts, example questions & explanations for Precalculus
All Precalculus Resources
Example Questions
Example Question #2 : Applying The Law Of Cosines
A triangle has sides of length 12, 17, and 22. Of the measures of the three interior angles, which is the greatest of the three?
We can apply the Law of Cosines to find the measure of this angle, which we will call :
The widest angle will be opposite the side of length 22, so we will set:
Example Question #2 : Triangles
In 
A triangle with these characteristics cannot exist.
By the Law of Cosines:
or, equivalently,
Substitute:
Example Question #1 : Trigonometric Graphs
What is the period of
The period for 
Example Question #14 : Graphs And Inverses Of Trigonometric Functions
Which of the following is not in the range of the function 
The range of the function 
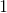
Of the choices given, 
Example Question #2 : Trigonometric Identities
What is the 
When working with basic trigonometric identities, it's easiest to remember the mnemonic: 
When one names the right triangle, the opposite side is opposite to the angle, the adjacent side is next to the angle, and the hypotenuse spans the two legs of the right angle.
Example Question #3 : Trigonometric Identities
What is the 
When working with basic trigonometric identities, it's easiest to remember the mnemonic: 
When one names the right triangle, the opposite side is opposite to the angle, the adjacent side is next to the angle, and the hypotenuse spans the two legs of the right angle.
Example Question #17 : Graphs And Inverses Of Trigonometric Functions
In a right triangle, if
and
then what does 
One can draw a right triangle with acute angles 
Example Question #51 : The Unit Circle And Radians
Bob manages a pizza store. He bought a new machine that tracks how big his employees are cutting the pizza slices. The machine measures the average angle size of each slice of each pizza. Unfortunately, the angle is given as 0.7854 radians which Bob does not understand. Help Bob by converting the radian angle into degrees. In degrees, what is the size of the angle for an average pizza slice.
To convert we use a common conversion amount. It may be easiest to remember the full circle example. In degrees, a full circle is 
Example Question #12 : Graphing The Sine And Cosine Functions
Convert 
To convert from degrees to radians, one multiplies by 
Example Question #52 : The Unit Circle And Radians
In the unit circle, what is the angle in radians that corresponds to the point (0, -1)?
On the unit circle, (0,-1) is the point that falls between the third and fourth quadrant. This corresponds to 
All Precalculus Resources
