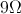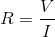A capacitor is an electrical device consisting of two parallel conducting plates that store charge. A capacitor undergoes two processes: charging and discharging. During charging, a capacitor accumulates and stores charge between the two plates. During discharge, a capacitor loses the stored charge. Since there is a decrease in the amount of charge during discharge, there is also a decrease (or decay) in current and voltage in a discharging capacitor. The decay of all these parameters is characterized by the equation:

Here,  and  denote the variable (voltage, current, or charge),  denotes the time elapsed,  denotes the resistance of the resistor, and  denotes the capacitance of the capacitor. This is an equation for exponential decay; therefore, all the variables undergo exponential decay in a discharging capacitor. 

The question states that the potential difference dropped from  to  in . The percentage of voltage drop is:

This means that there was a  voltage drop in . The definition of time constant is the time it takes for a capacitor to discharge to of its original value, or have a  drop; therefore, the time constant for this circuit is .

The time constant, tau, for an RC circuit is the product of the resistance of the resistor and the capacitance of the capacitor:

We can use this equation to solve for the resistance of the resistor:

Solving for resistance gives us:

Notice that you could have used the voltage decay equation to solve this problem; however, knowing the definition of time constant simplifies the problem and reduces the amount of calculations.

The equation for resistance is given by .

From this equation, we can see the best way to decrease resistance is by increasing the cross-sectional area, , of the cord. Increasing the length, , of the cord or the resistivity, , will increase the resistance.  

To relate resistance R, resistivity , area A, and length L we use the equation.

Rearranging to isolate the quantity we wish to solve for, L, gives the equation . We must first solve for A using the radius, 0.725mm.

Plugging in our numbers gives the answer, 960m.

Resistors in serries add according to the formula:

Resistors in parallel add according to the formula:

We can find the total equivalent resistance:

Now we can use Ohm's law to find the current:

Solve: 

To find resistance from voltage and current, we will need to use Ohm's law:

We are given the voltage and current, allowing us to solve for the resistance.

The student's hand on the sphere "grounds" it, allowing charges to flow in or out. No charge flows through the styrofoam insulator. When the negatively charged rod is brought nearby, negative charges in the sphere are repelled and exit via the student's hand, giving the sphere a net positive charge. After the student removes his hand, no more charges can flow into or out from the sphere, so the net positive charge remains after the rod is removed. Since this is a conducting sphere, the charges will spread out evenly over the surface.

Power is given in watts which is equal to 

Convert 10 minutes into seconds and then multiply the time in seconds with the number of watts to obtain the joules of energy required by the lightbulb.