All MCAT Physical Resources
Example Questions
Example Question #2 : Circuits
During the cold winter months, some gloves have the ability to provide extra warmth due to an internal heating source. A simplified circuit, similar to those in electric gloves, is comprised of a 9V battery with no internal resistance and three resistors as shown in the image below.

Instead of assuming that the 9V battery has no internal resistance, what would the terminal potential of the battery be if it has an internal resistance of 
Remember that internal resistance lowers the EMF of the battery. We need to calculate the voltage drop that would occur inside the battery, and then subtract that from the “stated” voltage to determine the terminal potential of the battery.
We first need the current supplied by the battery. We can use the formula V = IR because we have the voltage drop across the circuit (9V) and can calculate the equivalent resistance.
By taking the inverse of the equation, we can see that RA4 is equal to 2Ω.
Req = RA4 + R1 = 2Ω + 2Ω = 4Ω
Now, using V=IR, we can find the current in the circuit.
V = IR
I = V/R = 9V/4Ω = 2.25A
Plugging in this value with the internal resistance of the battery gives us the voltage decrease.
V = IR = (2.25A)(0.9Ω) = 2.025V
Terminal Potential = 9V – 2.025V = 6.975V
As we can see, battery companies are interested in keeping the internal resistance of batteries at a minimum, because it lowers the overall terminal potential of the battery.
Example Question #1 : Circuits
A circuit with two resistors (Resistor A and Resistor B) of equal resistance set up in parallel is attached to a battery with negligible internal resistance. Which of the following will occur if resistor B is removed?
(The wire of the circuit that resistor B is on will remain, however).
The voltage drop through resistor A will increase.
The voltage drop through resistor A will remain the same.
The voltage drop through resistor A will decrease.
The current through resistor A will increase.
The voltage drop through resistor A will remain the same.
For this question we need to know that the voltage drop is equal through all paths of a parallel circuit; therefore we can realize that the voltage drop through both resistors are independent of each other. The current through resistor A will decrease with the removal of resistor B. Electrons want to travel through the path of least resistance.
Example Question #1 : Circuits
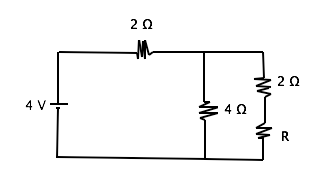
Given that the resistance of resisitor R = 2Ω, what is the voltage drop across the 4 Ω resistor in the circuit shown above?
4 V
1 V
2 V
0 .666 V
3.33 V
2 V
Given that resistor R = 2 Ω, we can see that the parallel aspect of the circuit has a resistance of 2 Ω as a whole, which means the total effective resistance of the circuit is 4 Ω. The potential difference drops 2V over the first resistor, then 2 V through the parallel aspect of the circuit. Potential difference, or voltage, drops through an equal amount in all branches of resistors in parallel. Therefore the remaining 2 V of potential difference is dropped by electrons moving through both branches of the parallel resistor, and the voltage drop through the 4 Ω resistor is 2V.
Example Question #1 : Voltage, Energy, And Power
What is the change in electrical potential energy for a charge of -2 µC moving through the circuit shown above?
2 µJ
16 µJ
–2 µJ
8 µJ
–8 µJ
–8 µJ
Given that
V(q) = U
When V is voltage, U is electrical potential energy and q is charge, we can solve by plugging in 4 for V and -2 for q. Also, we must understand that the electric potential energy of a particle decreases as it moves from an area of higher energy to one of lower energy. For an electron, it has higher energy in the negative terminal of the battery than it does in when getting to the positive terminal.
Example Question #41 : Electricity And Magnetism
During the cold winter months, some gloves have the ability to provide extra warmth due to an internal heating source. A simplified circuit, similar to those in electric gloves, is comprised of a 9 V battery with no internal resistance and three resistors as shown in the image below.

What is the voltage drop across the circuit?
4.5V
9V
0V
2.25V
9V
This question asks us directly about one of Kirchhoff’s Loop Laws—more specifically the second law that states that the sum of the voltage around any loop must be equal to zero.
ΣVcircuit = 0V
Because the battery provides 9V, the voltage drop across the circuit must be 9V.
As an aside, the other Kirchhoff Law, the first law, states that current into a junction must equal the current that exits the junction, due to conservation of charge.
Example Question #42 : Electricity And Magnetism
During the cold winter months, some gloves have the ability to provide extra warmth due to an internal heating source. A simplified circuit, similar to those in electric gloves, is comprised of a 9V battery with no internal resistance and three resistors as shown in the image below.

What is the voltage drop across RA?
First, we need to determine the voltage drop across R1, and then we can subtract that from the 9V battery to determine the voltage drop across RA. Given that RA and R4 are in parallel, we know that the voltage drop across each is the same.
The voltage drop across R1 can be calculated using the Icircuit (all the current generated by the battery’s potential difference must pass through R1 because it is in direct series with the battery), and the resistance of the resistor.
I can be calculated by V = IR because we have the voltage drop across the circuit (9V) and can calculate the equivalent resistance.
By taking the inverse of the equation, we can see that RA4 is equal to 2Ω.
Req = RA4 + R1 = 2Ω + 2Ω = 4Ω
Now, using V=IR allows us to find the current in the circuit.
V = IR
I = V/R = 9V/4Ω = 2.25 A
Plugging this value in, we can find the voltage drop across R1.
VR1 = IR = (2.25 A)(2Ω) = 4.5 V
Now we can determine the voltage drop across the parallel resistors by subtracting the voltage drop across R1 from the battery.
VA = 9V – 4.5V = 4.5V
Because RA and R4 are in parallel, the voltage drop across R4 is also 4.5V
Example Question #572 : Mcat Physical Sciences
A circuit consists of a 


Ohm's Law states that 
We also know that 
Finally, we know that 
Example Question #12 : Circuits
Suppose you have a circuit with two resistors connected in parallel. The first resistor (resistor A) has a resistance of 

Resistor A and resistor B will have the same power dissipation
Resistor A will have less power dissipation than resistor B
The relative power dissipation in the two resistors cannot be determined from the given information
Resistor A will have more power dissipation than resistor B
Resistor A will have less power dissipation than resistor B
Recall that circuit elements (such as resistors) connected in parallel have the same potential difference; therefore, resistor A and resistor B must have the same potential difference. Since we have information about the potential difference and the resistance of the two resistors, it would be best to use the equation for power in terms of voltage and resistance.
Since the potential difference is constant for both resistors, the power will only depend on the resistance. The equation implies that the power decreases when resistance is high; therefore, resistor A will have lower power dissipation than resistor B because resistor A has the greater resistance.
Example Question #11 : Circuits
Consider two resistors connected in series. The resistor with more power dissipation will likely have __________ potential difference and __________ resistance than the resistor with less power dissipation.
a larger . . . a smaller
the same . . . a larger
the same . . . a smaller
a larger . . . a larger
a larger . . . a smaller
Resistors connected in series will have the same current flowing through them, but will have different potential differences. Since we are concerned with the differences in potential difference and resistance, we need to use the power dissipation equation in terms of voltage and resistance:
The equation implies that there will be a greater power dissipation when the potential difference increases and the resistance decreases. A resistor undergoing greater power dissipation will most likely have a higher potential difference and lower resistance.
Example Question #44 : Electricity And Magnetism
Which of the following is false regarding power dissipation in an electrical circuit?
I. A decrease in power dissipation across a resistor means more of the electrical energy is converted to heat
II. Power dissipation always decreases as the resistance of a resistor increases
III. Electrical power could be measured in units of "volt-amperes"
I and II
II and III
III only
I, II, and III
I and II
Power dissipation is defined as the ability of a circuit element (such as a resistor) to convert the electrical energy to other forms of energy, such as heat or mechanical energy. This means that a decrease in power dissipation will convert less of the electrical energy to heat and mechanical energy. Statement I is false (and therefore a correct answer choice).
Electrical power can be written in terms of voltage (


Notice that resistance is in the numerator in the first equation and in the denominator in the second equation; therefore, the power doesn’t always decrease when resistance increases. It depends on the equation used to calculate the power. Statement II is false (and therefore a correct answer choice).
Amperes is the unit of current and volts is the unit of voltage; therefore, we need to find the equation for power in terms of voltage and current to determine if power can be measured in volt-amperes. The equation for power in terms of voltage and current is:
Power can be measured in the units of volt-amperes (VA). Statement III is true (and therefore an incorrect answer option).
Certified Tutor
All MCAT Physical Resources