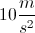We must first determine the amount of time that the ball is in the air, then use the horizontal velocity to solve for the distance travelled.

In order to solve for the amount of time, we need to know the vertical initial velocity of the cannonball. This is given by the equation . Using the initial velocity of  we determine that the vertical initial velocity is 

Knowing this, we can solve the amount of time it will take for the cannon ball to reach its maximum peak, with a velocity of  using the equation 

This is the amount of time it takes for the ball to reach its peak, not the total time it is in the air. Since the ball must drop from the maximum height, we double the time and find that total flight time is 20.8s.

The next step is determining the horizontal initial velocity from the cannon. This is determined using the equation below.

Since we assume that there is no air resistance, we can conclude that the horizontal velocity of the cannonball will remain constant throughout its flight. As a result, the total displacement equation is simplified to the following: .

First, solve for the initial vertical velocity of the ball.

v_y = (10m/s)(sin(45^o)) = 7.1m/s

Think back to the 3 main kinematics equations we know:

v_f² = v_i² + 2aΔx

v_f = v_i + at

Δx = v_it + ½at²

We need to choose an equation that allows us to solve for the vertical height of the ball, given that we know the initial vertical velocity, final vertical velocity (zero), and the acceleration due to gravity (-9.8m/s²).

v_f² = v_i² + 2aΔy

Δy = (v_f² - v_i²)/2a

Once again, think back to our 3 main kinematics question:

v_f²  = v_i² + 2aΔx

v_f = v_i + at

Δx = v_it + ½at²

We want an equation that allows us to determine the time the ball spends in flight. Often, it is easier to compute the time it takes for the ball to reach its maximum height, then multiply by two. However, this “shortcut” only works when the launch point and end point are at the same vertical height, as they are in this problem.

v_f = v_i + at

t = (v_f – v_i)/a

Remember to use the veritcal velocity as your initial velocity.

v_y = (10m/s)(sin(45^o)) = 7.1m/s

This is one half of the flight time. We multiply by two to find the total time.

t = 2(0.72s) = 1.44s

First, we will need the time that the ball is in flight.

Think back to our 3 main kinematics question:

v_f²  = v_i² + 2aΔx

v_f = v_i + at

Δx = v_it + ½at²

We want an equation that allows us to determine the time the ball spends in flight. Often, it is easier to compute the time it takes for the ball to reach its maximum height, then multiply by two. However, this “shortcut” only works when the launch point and end point are at the same vertical height, as they are in this problem.

v_f = v_i + at

t = (v_f – v_i)/a

Remember to use the veritcal velocity as your initial velocity.

v_y = (10m/s)(sin(45^o)) = 7.1m/s

This is one half of the flight time. We multiply by two to find the total time.

t = 2(0.72s) = 1.44s

Using this time with the initial horizontal velocity will allow us to solve for the total horizontal distance.

 v_x = (10m/s)(cos(45^o)) = 7.1m/s

Δx = v_it + ½at²

Δx = (7.1m/s)(1.44s) = 10.22m

This question asks us to consider gravitational potential energy. We are provided the mass of the ball (2kg) and know the acceleration due to gravity (9.8m/s²). Using the height of the ball at the top of its arc, we can solve for gravitational potential energy.

First, solve for the initial vertical velocity of the ball.

v_y = (10m/s)(sin(45^o)) = 7.1m/s

Think back to the 3 main kinematics equations we know:

v_f² = v_i² + 2aΔx

v_f = v_i + at

Δx = v_it + ½at²

We need to choose an equation that allows us to solve for the vertical height of the ball, given that we know the initial vertical velocity, final vertical velocity (zero), and the acceleration due to gravity (-9.8m/s²).

v_f² = v_i² + 2aΔy

Δy = (v_f² - v_i²)/2a

Now that we know the maximum height, we can find the potential energy from this position.

U = mgh

U = (2kg)(9.8m/s²)(2.57m) = 50.4J

To find the acceleration of the box traveling down the incline, the mass is not needed. Using the incline of the plane as the x-direction, we can see that there is no movement in the y-direction; therefore, we can use Newton's second, F = ma, in the x-direction.

There is only one force in the x-direction (gravity), however gravity is not just equal to “mg” in this case. Since the box is on an incline, the gravitational force will be equal to mgsin(30^o). Substituting force into F  =ma we find that mgsin(30^o) = ma. We can now cancel out masses and solve for acceleration.

Consider a triangle in which the initial velocity is the hypotenuse. The horizontal component of the velocity can be found using trigonometry:

Use our given values to solve:

Displacement is the change in from intial position to final position. The car first travels 30 miles east and then returns 3 miles west.

East:

West:

They have traveled 27 miles east from their initial position.

The force of gravity on the box will be in the downward direction, but the acceleration generated will be parallel to the surface of the incline. We can break the total force of gravity into parallel (horizontal) and perpendicular (vertical) components.

Calculate the horizontal force on the box.

Now that we know the horizontal force, we can solve for the horizontal acceleration by using the mass of the box and Newton's second law.