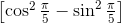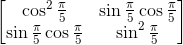Call Now to Set Up Tutoring:

(888) 888-0446

Linear Algebra : Linear Algebra

Study concepts, example questions & explanations for Linear Algebra

Create An Account

All Linear Algebra Resources

4 Diagnostic Tests 108 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #781 : Linear Algebra

Let $A= \begin{bmatrix} \frac{3}{2} & \frac{1}{4} \\ \\ \frac{3}{4} &- \frac{1}{5}\end{bmatrix}$ and $B = \begin{bmatrix} \frac{2}{5} & \frac{1}{4}\end{bmatrix}$ .

Find .

Possible Answers:

$\begin{bmatrix} \frac{53}{80} & \frac{1}{4} \end{bmatrix}$

is undefined.

$\begin{bmatrix} \frac{63}{80} \\ \\ \frac{1}{20} \end{bmatrix}$

$\begin{bmatrix} \frac{53}{80} \\ \\ \frac{1}{4} \end{bmatrix}$

$\begin{bmatrix} \frac{63}{80} & \frac{1}{20} \end{bmatrix}$

Correct answer:

is undefined.

Explanation:

First, it must be established that is defined. This is the case if and only if has as many columns as has rows. Since has two columns and has one row, is not defined.

Report an Error

Example Question #781 : Linear Algebra

$A=\begin{bmatrix} a & 1 \\ 1 & 1\end{bmatrix}$ and $B = \begin{bmatrix} b & 1 \\ 1 & 1 \end{bmatrix}$ , where and stand for real quantities.

Which of the following must be a true statement?

Possible Answers:

$BA = (AB)^{T}$

$BA = -(AB)^{T}$

BA = AB

None of the statements given in the other choices are correct.

BA = -(AB)

Correct answer:

$BA = (AB)^{T}$

Explanation:

Matrices are multiplied by multiplying each row of the first matrix by each column of the second - that is, by adding the products of the entries in corresponding positions. Thus,

$AB=\begin{bmatrix} a & 1 \\ 1 & 1\end{bmatrix}\begin{bmatrix} b & 1 \\ 1 & 1 \end{bmatrix}$

$= \begin{bmatrix} a(b)+ 1(1) & a(1)+1(1) \\ 1(b)+ 1(1) & 1(1)+1(1) \end{bmatrix}$

$= \begin{bmatrix} ab+1 &a+1 \\ b+1 & 2 \end{bmatrix}$

$BA=\begin{bmatrix} b & 1 \\ 1 & 1\end{bmatrix}\begin{bmatrix}a & 1 \\ 1 & 1 \end{bmatrix}$

$= \begin{bmatrix} b(a)+ 1(1) & b(1)+1(1) \\ 1(a)+ 1(1) & 1(1)+1(1) \end{bmatrix}$

$= \begin{bmatrix} ab+1 &b+1 \\ a+1 & 2 \end{bmatrix}$

If rows and columns are transposed in , it can be seen that

$(AB)^{T}= \begin{bmatrix} ab+1 &b+1 \\ a+1 & 2 \end{bmatrix} = BA$ .

Report an Error

Example Question #782 : Linear Algebra

$A=\begin{bmatrix}1 & a \\-a & 1\end{bmatrix}$ and $B = \begin{bmatrix} 1 & b \\ -b& 1 \end{bmatrix}$ , where and stand for real quantities.

Which of the following must be a true statement?

Possible Answers:

BA = -AB

None of the statements given in the other choices are correct.

BA = AB

$BA = -(AB)^{T}$

$BA = (AB)^{T}$

Correct answer:

BA = AB

Explanation:

Matrices are multiplied by multiplying each row of the first matrix by each column of the second - that is, by adding the products of the entries in corresponding positions. Thus,

$AB=\begin{bmatrix}1 & a \\-a & 1\end{bmatrix} \begin{bmatrix} 1 & b \\ -b& 1 \end{bmatrix}$

$=\begin{bmatrix}1 (1)+a(-b)& 1 (b)+a(1) \\-a (1)+1(-b)& -a (b)+1(1) \end{bmatrix}$

$=\begin{bmatrix}-ab+1&a+b\\-a -b& -ab+1 \end{bmatrix}$

$BA=\begin{bmatrix}1 & b \\-b & 1\end{bmatrix} \begin{bmatrix} 1 & a \\ -a& 1 \end{bmatrix}$

$=\begin{bmatrix}1 (1)+b(-a)& 1 (a)+b(1) \\-b (1)+1(-a)& -b(a)+1(1) \end{bmatrix}$

$=\begin{bmatrix}-ab+1&a+b\\-a -b& -ab+1 \end{bmatrix}$

= AB

Report an Error

Example Question #781 : Linear Algebra

$A^{2}$ is a symmetric matrix.

True or false: It follows that is also a symmetric matrix.

Possible Answers:

False

True

Correct answer:

False

Explanation:

This statement can be proved by counterexample.

Let $A= \begin{bmatrix} 6 & -5\\ 7& -6 \end{bmatrix}$ .

is not symmetric, since its transpose,

$A^{T}= \begin{bmatrix} 6 & 7\\ -5& -6 \end{bmatrix}$

is not equal to .

Then

$A^{2}= \begin{bmatrix} 6 & -5\\ 7& -6 \end{bmatrix}\begin{bmatrix} 6 & -5\\ 7& -6 \end{bmatrix}$

Matrices are multiplied by multiplying each row of the first matrix by each column of the second - that is, by adding the products of the entries in corresponding positions. Thus,

$A^{2} = \begin{bmatrix} 6(6)+(-5)(7) &6(-5)+(-5)(-6) \\ 7(6)+(-6)(7) &7(-5)+(-6)(-6) \end{bmatrix}= \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$ .

Therefore, $A^{2}= I$ , the two-by-two identity, which is symmetric.

Since a nonsymmetric matrix exists whose square is symmetric, then the given statement is false.

Report an Error

Example Question #783 : Linear Algebra

$A= \begin{bmatrix} i & 0 & 0 \\ 0 &0 &-i\end{bmatrix}$

Calculate $A^{20 }$ .

Possible Answers:

$A^{20 }$ is undefined.

$\begin{bmatrix} i & 0 & 0 \\ 0 &0 &-i\end{bmatrix}$

$\begin{bmatrix}-1 & 0 & 0 \\ 0 &0 &-1\end{bmatrix}$

$\begin{bmatrix}1 & 0 & 0 \\ 0 &0 &1\end{bmatrix}$

$\begin{bmatrix} i & 0 & 0 \\ 0 &0 &i\end{bmatrix}$

Correct answer:

$A^{20 }$ is undefined.

Explanation:

Only square matrices can be taken to any power. Since is not a square matrix, having two rows and three columns, $A^{20 }$ is undefined.

Report an Error

Example Question #782 : Linear Algebra

$A= \begin{bmatrix} i & 0 & 0 \\ 0 &0 &-i\end{bmatrix}$

Calculate $(A^{T}A)^{77}$ .

Possible Answers:

$\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1& 0 \\ 0 & 0 & 1 \end{bmatrix}$

$\begin{bmatrix} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{bmatrix}$

None of the other choices gives the correct response.

$\begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix}$

$\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$

Correct answer:

None of the other choices gives the correct response.

Explanation:

$A^{T}$ , the transpose of , can be found by transposing rows with columns.

$A= \begin{bmatrix} i & 0 & 0 \\ 0 &0 &-i\end{bmatrix}$ , so

$A^{T}= \begin{bmatrix} i & 0 \\0& 0 \\ 0 &-i\end{bmatrix}$

Matrices are multiplied by multiplying each row of the first matrix by each column of the second - that is, by adding the products of the entries in corresponding positions. Thus,

$A^{T}A= \begin{bmatrix} i & 0 \\0& 0 \\ 0 &-i\end{bmatrix} \begin{bmatrix} i & 0 & 0 \\ 0 &0 &-i\end{bmatrix}$

$= \begin{bmatrix} i(i)+ 0(0) & i(0)+ 0(0) & i(0)+ 0(-i) \\ 0(i)+ 0(0) & 0(0)+ 0(0) & 0(0)+ 0(-i) \\ 0(i)+ (-i)(0) &0(0)+ (-i)(0) & 0(0)+ (-i)(-i) \end{bmatrix}$

$=\begin{bmatrix} -1 & 0 & 0 \\ 0 &0 & 0 \\ 0 & 0 & -1 \end{bmatrix}$

This is a square matrix, so it can be raised to a power. To raise a diagonal matrix to a power, simply raise each number in the main diagonal to that power:

$(A^{T}A)^{77} =\begin{bmatrix} (-1)^{77} & 0 & 0 \\ 0 &0^{77} & 0 \\ 0 & 0 & (-1)^{77} \end{bmatrix}=\begin{bmatrix} -1 & 0 & 0 \\ 0 &0 & 0 \\ 0 & 0 & -1 \end{bmatrix}$ .

This is not among the choices.

Report an Error

Example Question #782 : Linear Algebra

$A= \begin{bmatrix} i & 0 & 0 \\ 0 &0 &-i\end{bmatrix}$

Calculate $(AA^{T})^{99}$ .

Possible Answers:

$\begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix}$

$\begin{bmatrix} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \end{bmatrix}$

$(AA^{T})^{99}$ is not defined.

$\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1& 0 \\ 0 & 0 & 1 \end{bmatrix}$

$\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$

Correct answer:

$\begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix}$

Explanation:

$A^{T}$ , the transpose of , can be found by transposing rows with columns.

$A= \begin{bmatrix} i & 0 & 0 \\ 0 &0 &-i\end{bmatrix}$ , so

$A^{T}= \begin{bmatrix} i & 0 \\0& 0 \\ 0 &-i\end{bmatrix}$

Matrices are multiplied by multiplying each row of the first matrix by each column of the second - that is, by adding the products of the entries in corresponding positions. Thus,

$A A^{T}= \begin{bmatrix} i & 0 & 0 \\ 0 &0 &-i\end{bmatrix} \begin{bmatrix} i & 0 \\0& 0 \\ 0 &-i\end{bmatrix}$

$= \begin{bmatrix} i (i)+ 0(0)+ 0(0) & i(0)+ 0(0)+ 0(-i) \\ 0(i)+ 0(0)+ (-i)(0) & 0(0)+ 0(0)+ (-i)(-i) \end{bmatrix}$

$= \begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix}$

This is a square matrix, so it can be raised to a power. To raise a diagonal matrix to a power, simply raise each number in the main diagonal to that power:

$(AA^{T})^{99} = \begin{bmatrix} (-1)^{99} & 0 \\ 0 & (-1)^{99} \end{bmatrix}= \begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix}$ .

Report an Error

Example Question #783 : Linear Algebra

$A=\begin{bmatrix} a & 1 \\ -1 & b \end{bmatrix}$ and $C = \begin{bmatrix} c & -1 \\ 1 & d \end{bmatrix}$ , where all four variables stand for real quantities.

Which must be true of and regardless of the values of the variables?

Possible Answers:

AC= CA

$AC= -(CA)^{T}$

AC=- (CA)

$AC= (CA)^{T}$

None of the statements given in the other choices are correct.

Correct answer:

None of the statements given in the other choices are correct.

Explanation:

Matrices are multiplied by multiplying each row of the first matrix by each column of the second - that is, by adding the products of the entries in corresponding positions. Thus,

$AC=\begin{bmatrix} a & 1 \\ -1 & b \end{bmatrix}\begin{bmatrix} c & -1 \\ 1 & d \end{bmatrix}$

$=\begin{bmatrix} a (c)+ 1(1)& a (-1)+ 1(d)\\ -1 (c)+ b(1)& -1 (-1)+ b(d)\end{bmatrix}$

$=\begin{bmatrix} ac+1&-a+d \\ b-c& bd+1\end{bmatrix}$

$CA=\begin{bmatrix} c & -1 \\ 1 & d \end{bmatrix}\begin{bmatrix} a & 1 \\ -1 & b \end{bmatrix}$

$=\begin{bmatrix} c (a)+ (-1)(-1)& c(1)+(-1)(b)\\ 1 (a)+ d(-1)& 1(1)+d(b)\end{bmatrix}$

$=\begin{bmatrix} ac+1& -b+c\\ a-d& bd+1\end{bmatrix}$

AC= CA is false in general.

$(CA)^{T}$ , the transpose of , is the result of transposing rows and columns:

$(CA)^{T} =\begin{bmatrix} ac+1& a-d \\ -b+c & bd+1\end{bmatrix}$ . so

$AC= (CA)^{T}$ is false in general.

$-(CA) =\begin{bmatrix} -ac-1& b-c\\ -a-d&- bd-1\end{bmatrix}$ , so

AC=- (CA) is false in general.

$-(CA)^{T} =\begin{bmatrix} -ac-1&-a-d \\ b-c &- bd-1\end{bmatrix}$ , so

$AC= -(CA)^{T}$ is false in general.

Thus, none of the four given statements need be true.

Report an Error

Example Question #783 : Linear Algebra

Let $A = \begin{bmatrix} \cos \frac{\pi }{5} \\ \sin \frac{\pi }{5} \end{bmatrix}$

Find $(AA^{T})^{2}$ .

Possible Answers:

$\begin{bmatrix} \cos ^{2}\frac{\pi }{5} & 1 \\ 1& \sin^{2} \frac{\pi }{5}\end{bmatrix}$

$\begin{bmatrix} \cos ^{2}\frac{\pi }{5} & \sin \frac{\pi }{5}\cos \frac{\pi }{5} \\ \sin \frac{\pi }{5}\cos \frac{\pi }{5} & \sin^{2} \frac{\pi }{5}\end{bmatrix}$

$\begin{bmatrix} \cos ^{2}\frac{\pi }{5} - \sin^{2} \frac{\pi }{5}\end{bmatrix}$

$\begin{bmatrix} 1 \end{bmatrix}$

$(AA^{T})^{2}$ is undefined.

Correct answer:

$\begin{bmatrix} \cos ^{2}\frac{\pi }{5} & \sin \frac{\pi }{5}\cos \frac{\pi }{5} \\ \sin \frac{\pi }{5}\cos \frac{\pi }{5} & \sin^{2} \frac{\pi }{5}\end{bmatrix}$

Explanation:

is equal to the two-entry column matrix $\begin{bmatrix} \cos \frac{\pi }{5} \\ \sin \frac{\pi }{5} \end{bmatrix}$ , so $A^{T}$ , the transpose, is the row matrix

$A^{T} = \begin{bmatrix} \cos \frac{\pi }{5} & \sin \frac{\pi }{5} \end{bmatrix}$

The product of two matrices is calculated by multiplying rows by columns - adding the corresponding entries in the rows of the first matrix by the columns of the second - so

$AA^{T}= \begin{bmatrix} \cos \frac{\pi }{5} \\ \sin \frac{\pi }{5} \end{bmatrix}\begin{bmatrix} \cos \frac{\pi }{5} & \sin \frac{\pi }{5} \end{bmatrix}$

$= \begin{bmatrix} \cos \frac{\pi }{5}(\cos \frac{\pi }{5}) & \sin \frac{\pi }{5}(\cos \frac{\pi }{5}) \\ \cos \frac{\pi }{5}(\sin \frac{\pi }{5}) & \sin \frac{\pi }{5}(\sin \frac{\pi }{5}) \end{bmatrix}$

$= \begin{bmatrix} \cos ^{2}\frac{\pi }{5} & \sin \frac{\pi }{5}\cos \frac{\pi }{5} \\ \sin \frac{\pi }{5}\cos \frac{\pi }{5} & \sin^{2} \frac{\pi }{5}\end{bmatrix}$

Report an Error

Example Question #1 : Matrix Vector Product

Multiply: $\begin{bmatrix} 2 & 0& -5\\ -1& 3& 1\end{bmatrix} \cdot \begin{bmatrix} 2\\ 2\\ 1\end{bmatrix}$

Possible Answers:

$\begin{bmatrix} -1\\5 \end{bmatrix}$

$\begin{bmatrix} 9\\5 \end{bmatrix}$

$\begin{bmatrix} -1\\ -3\end{bmatrix}$

$\begin{bmatrix} 9\\8 \end{bmatrix}$

$\begin{bmatrix} -1\\8 \end{bmatrix}$

Correct answer:

$\begin{bmatrix} -1\\5 \end{bmatrix}$

Explanation:

To multiply, add:

$2 \begin{bmatrix} 2\\ -1\end{bmatrix} + 2 \begin{bmatrix} 0\\3 \end{bmatrix} + 1 \begin{bmatrix} -5\\ 1\end{bmatrix}$

$= \begin{bmatrix} 4\\-2 \end{bmatrix} + \begin{bmatrix} 0\\ 6\end{bmatrix} + \begin{bmatrix} -5\\ 1\end{bmatrix} = \begin{bmatrix} -1\\ 5\end{bmatrix}$

Report an Error

View Linear Algebra Tutors

Chelsea
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Physics. The University of Texas at Dallas, Master of Science, Bioinf...

View Linear Algebra Tutors

Ravi
Certified Tutor

Indian Institute of Technology - Mumbai, Bachelor of Technology, Mechanical Engineering. University of Cincinnati-Main Campus...

View Linear Algebra Tutors

Pritam
Certified Tutor

University of Washington-Seattle Campus, Bachelor of Engineering, Electrical Engineering.

All Linear Algebra Resources

4 Diagnostic Tests 108 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Calculus Tutors in Boston, Calculus Tutors in Washington DC, GRE Tutors in New York City, Chemistry Tutors in Houston, SAT Tutors in Chicago, SAT Tutors in Washington DC, Chemistry Tutors in Seattle, MCAT Tutors in Denver, Biology Tutors in Los Angeles, Spanish Tutors in Phoenix

Popular Courses & Classes

SSAT Courses & Classes in San Francisco-Bay Area, MCAT Courses & Classes in Boston, ACT Courses & Classes in Denver, ISEE Courses & Classes in Seattle, SAT Courses & Classes in Philadelphia, SSAT Courses & Classes in Seattle, GMAT Courses & Classes in Houston, LSAT Courses & Classes in Boston, SAT Courses & Classes in Denver, GRE Courses & Classes in Chicago

Popular Test Prep

SSAT Test Prep in Chicago, ISEE Test Prep in San Francisco-Bay Area, SSAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in Houston, SSAT Test Prep in Miami, MCAT Test Prep in Seattle, LSAT Test Prep in Denver, ACT Test Prep in Miami, GRE Test Prep in Houston, SAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Linear Algebra : Linear Algebra

Study concepts, example questions & explanations for Linear Algebra

All Linear Algebra Resources

Example Questions

Example Question #781 : Linear Algebra

Example Question #781 : Linear Algebra

Example Question #782 : Linear Algebra

Example Question #781 : Linear Algebra

Example Question #783 : Linear Algebra

Example Question #782 : Linear Algebra

Example Question #782 : Linear Algebra

Example Question #783 : Linear Algebra

Example Question #783 : Linear Algebra

Example Question #1 : Matrix Vector Product

All Linear Algebra Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: