All Linear Algebra Resources
Example Questions
Example Question #122 : Matrices
Let 

Find the product 
The product does not exist because the dimensions do not match.
The product does not exist because the dimensions do not match.
The matrix 

Example Question #123 : Matrices
Rewrite the system of equations:
into a matrix vector product:
where 
3x3 matrix and


To write
into matrix vector form, we recall that matrix multiplication with a vector is done such that the first element in the resulting vector is the dot product of the first row of 





The right side is the vector 
which is equivalent to
Example Question #124 : Matrices
Let 

Find 

First, it must be established that 





Matrices are multiplied by multiplying each row of the first matrix by each column of the second - that is, by adding the products of the entries in corresponding positions. Thus,
Example Question #21 : Matrix Vector Product
Multiply
To multiply, add:
Example Question #1 : Vector Vector Product
Compute 
Not possible
Before we compute the product of 






Example Question #121 : Matrices
Find the vector-vector product of the following vectors.
It's not possible to multiply these vectors
Example Question #2 : Vector Vector Product
Calculate 
By definition,
![\textbf{A} \times \textbf{B} = \begin{vmatrix} \hat{i}& \hat{j}&\hat{k} \\ 4& -2& 0\\ 1& 3& 0 \end{vmatrix} =\hat{i}(0)-\hat{j}(0)+\hat{k}[4(3)-1(-2)] = 14 \hat{k}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/800856/gif.latex)
Example Question #2 : Vector Vector Product
What is the physical significance of the resultant vector 














By definition, the resultant cross product vector (in this case, 






Example Question #133 : Matrices
Example Question #3 : Vector Vector Product
Certified Tutor
All Linear Algebra Resources







































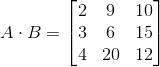


![A=[1 \ 2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/727325/gif.latex)



























