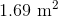All ISEE Middle Level Quantitative Resources
Example Questions
Example Question #1 : Coordinate Geometry
The ordered pair 
Quadrant II
Quadrant I
Quadrant IV
Quadrant V
Quadrant III
Quadrant II
There are four quadrants in the coordinate plane. Quadrant I is the top right, and they are numbered counter-clockwise. Since the x-coordinate is 

Example Question #10 : Coordinate Geometry
If angles s and r add up to 180 degrees, which of the following best describes them?
Acute
Obtuse
Supplementary.
Complementary
Supplementary.
Two angles that are supplementary add up to 180 degrees. They cannot both be acute, nor can they both be obtuse. Therefore, "Supplementary" is the correct answer.
Example Question #11 : Geometry
The lines of the equations
and
intersect at a point 
Which is the greater quantity?
(a)
(b)
(a) and (b) are equal
It is impossible to determine which is greater from the information given
(b) is the greater quantity
(a) is the greater quantity
(b) is the greater quantity
If 

Substitute:
Example Question #1 : Quadrilaterals
Calvin is remodeling his room. He used 


When Calvin put up 





In order to solve for 
The left-hand side simplifies to:
The right-hand side simplifies to:
Now, Calvin knows the width of each room is 



Since Calvin wants to find how much paint he needs to cover three walls, he must first find out how many square feet he is covering. If one wall is 

Calvin is painting 


Calvin will need 
Example Question #1 : Plane Geometry
Which is the greater quantity?
(a) The surface area of a cube with volume
(b) The surface area of a cube with sidelength
(a) is greater
It is impossible to tell from the information given
(a) and (b) are equal
(b) is greater
(b) is greater
We can actually solve this by comparing volumes; the cube with the greater volume has the greater sidelength and, subsequently, the greater surface area.
The volume of the cube in (b) is the cube of 90 millimeters, or 9 centimeters. This is 

Example Question #3 : Plane Geometry
The sum of the lengths of three sides of a square is one yard. Give its area in square inches.
A square has four sides of the same length.
One yard is equal to 36 inches, so each side of the square has length

Its area is the square of the sidelength, or

Example Question #4 : Plane Geometry
The sum of the lengths of three sides of a square is 3,900 centimeters. Give its area in square meters.
100 centimeters are equal to one meter, so 3,900 centimeters are equal to

A square has four sides of the same length. Since the sum of the lengths of three of the congruent sides is 3,900 centimeters, or 39 meters, each side measures

The area of the square is the square of the sidelength, or

Example Question #5 : Plane Geometry
Each side of a square is 
(A) The area of the square
(B)
(B) is greater
(A) and (B) are equal
It is impossible to determine which is greater from the information given
(A) is greater
It is impossible to determine which is greater from the information given
The area of a square is the square of its side length:
Using the side length from the question:
However, it is impossible to tell with certainty which of 

For example, if 
and
so 

But if 
and
so 

Example Question #6 : Plane Geometry
A square has a side with a length of 5. What is the area of the square?
The area formula for a square is length times width. Keep in mind that all of a square's sides are equal.
So, if one side of a square equals 5, all of the other sides must also equal 5. You will find the area of the square by multiplying two of its sides:
Example Question #2 : Plane Geometry
One square mile is equivalent to 640 acres. Which of the following is the greater quantity?
(a) The area of a square plot of land whose perimeter measures one mile
(b) 160 acres
(a) and (b) are equal
(b) is the greater quantity
It is impossible to determine which is greater from the information given
(a) is the greater quantity
(b) is the greater quantity
A square plot of land with perimeter one mile has as its sidelength one fourth of this, or 

One square mile is equivalent to 640 acres, so 

This makes (b) greater.
All ISEE Middle Level Quantitative Resources