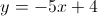ISEE Middle Level Quantitative : ISEE Middle Level (grades 7-8) Quantitative Reasoning
Study concepts, example questions & explanations for ISEE Middle Level Quantitative
All ISEE Middle Level Quantitative Resources
Example Questions
Example Question #2 : How To Find The Missing Part Of A List
Five candidates are running for school board. A voter chooses two of the candidates.
Which is the greater quantity?
(a) The number of ways a voter can mark his or her ballot
(b)
(a) and (b) are equal
(a) is greater
It is impossible to tell from the information given
(b) is greater
(b) is greater
This is a choice of two out of five without regard to order - that is, the number of combinations of two out of a set of five. This is
There are ten possible ways to choose, and 
Example Question #10 : Sets
Refer to the above diagram. The top row gives a sequence of figures. Which figure on the bottom row comes next?
Figure (c)
Figure (d)
Figure (a)
Figure (b)
Figure (c)
The square with the diagonal line alternates between the square on the left and the square on the right. Therefore, the next figure in the sequence will have its diagonal line in the rightmost square, eliminating Figures (b) and (d) and leaving Figures (a) and (c).
Also, the shaded square moves one position to the right from figure to figure, so in the next figure, the shaded square must be the one at the extreme right. Figure (c) matches that description.
Example Question #391 : Isee Middle Level (Grades 7 8) Quantitative Reasoning
Give the equation of the line through point 
Use the point-slope formula with
Example Question #1 : Geometry
Which is the greater quantity?
(A) The slope of the line
(B) The slope of the line
(A) is greater
It is impossible to determine which is greater from the information given
(B) is greater
(A) and (B) are equal
(A) is greater
Rewrite each in the slope-intercept form, 
The slope of this line is 
The slope of this line is 
Since 
Example Question #392 : Isee Middle Level (Grades 7 8) Quantitative Reasoning
Which is the greater quantity?
(A) The slope of the line
(B) The slope of the line
(A) and (B) are equal
It is impossible to determine which is greater from the information given
(B) is greater
(A) is greater
(A) and (B) are equal
Rewrite each in the slope-intercept form,
The slope of the line of 
The slope of the line of 
The slopes are equal.
Example Question #2 : Geometry
(a) The slope of the line on the coordinate plane through the points 
(b) The slope of the line on the coordinate plane through the points 
(b) is the greater quantity
It is impossible to determine which is greater from the information given
(a) and (b) are equal
(a) is the greater quantity
(a) and (b) are equal
The slope of a line through the points 
in the slope formula:
The slope of a line through the points 
The lines have the same slope.
Example Question #1 : Geometry
A line passes through the points with coordinates 
Undefined
The slope of a line through the points 
in the slope formula:
Example Question #393 : Isee Middle Level (Grades 7 8) Quantitative Reasoning
Choose the best answer from the four choices given.
The point (15, 6) is on which of the following lines?
For this problem, simply plug in the values for the point (15,6) into the different equations (15 for the 
Example Question #1 : How To Find The Points On A Coordinate Plane
Choose the best answer from the four choices given.
What is the point of intersection for the following two lines?
At the intersection point of the two lines the 
point of intersection
Example Question #1 : Geometry
Choose the best answer from the four choices given.
What is the 
In the formula 
Thus, to find the 
All ISEE Middle Level Quantitative Resources
