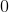Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : Other Lines

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #35 : How To Find The Equation Of A Line

Find the equation of a line that passes through the following points:

(5, 8) and (6, 12)

Possible Answers:

$y=\frac{17}{14}x-2$

y=-4x-8

y=4x-12

y=3x-2

$y=\frac{1}{4}x-10$

Correct answer:

y=4x-12

Explanation:

Recall that the the following is the slope-intercept form of a line:

y=mx+b

In this equation, the variables are represented by the following:

$m=\text{slope}$

$b=\text{y-intercept}$

Find the slope of the line by using the following formula:

$\text{Slope of Line}=\frac{y_2-y_1}{x_2-x_1}$

In this equation, the x- and y-variables correspond to the coordinates of the given points.

$\text{Slope}=\frac{12-8}{6-5}$

$\text{Slope}=\frac{4}{1}$

$\text{Slope}=4$

Next, find the y-intercept of the line by substituting one of the points into the semi-completed formula.

y=4x+b

Substituting in the point (5, 8) yields the following:

8=4(5)+b

Rearrange and solve for .

b+20=8

Subtract 20 from both sides of the equation.

b+20-20=8-20

b=-12

Substitute this value of the y-intercept into our semi-complete equation to get the answer:

y=4x-12

Report an Error

Example Question #63 : Expressions & Equations

What is the slope of the line that passes through the points (3,4) and (5,13) ?

Possible Answers:

-9/2

13/4

2/9

-4/3

9/2

Correct answer:

9/2

Explanation:

The slope of a line is sometimes referred to as "rise over run." This is because the formula for slope is the change in y-value (rise) divided by the change in x-value (run). Therefore, if you are given two points, $(x_{1},y_{1})$ and $(x_{2},y_{2})$ , the slope of their line can be found using the following formula: $slope=(y_{1}-y_{2})/(x_{1}-x_{2})$

This gives us (13-4)/(5-3)=9/2 .

Report an Error

Example Question #1 : Graph Proportional Relationships, Interpreting The Unit Rate As The Slope: Ccss.Math.Content.8.Ee.B.5

Given points (1,2) and (-1,3) , what is the slope of the line connecting them?

Possible Answers:

$-\frac{1}{2}$

$\frac{1}{2}$

$-\frac{1}{4}$

Correct answer:

$-\frac{1}{2}$

Explanation:

Write the slope formula. Plug in the points and solve.

$m= \frac{y_2-y_1}{x_2-x_1}= \frac{3-2}{-1-1}= -\frac{1}{2}$

Report an Error

Example Question #2 : Graph Proportional Relationships, Interpreting The Unit Rate As The Slope: Ccss.Math.Content.8.Ee.B.5

What is the slope of the line connecting the points $(2,\sqrt2)$ and (1,2) ?

Possible Answers:

$\sqrt2 -2$

$-\sqrt2+1$

$-\sqrt2-2$

$2-\sqrt2$

$-1-\sqrt2$

Correct answer:

$\sqrt2 -2$

Explanation:

Write the slope formula. Plug in the point, and simplify.

$m=\frac{y_2-y_1}{x_2-x_1}= \frac{2-\sqrt2}{1-2}=\frac{2-\sqrt2}{-1}= -(2-\sqrt2) = \sqrt2-2$

Report an Error

Example Question #66 : Expressions & Equations

What is the slope of a line with an -intercept is and another -intercept of ?

Possible Answers:

$\infty$

Correct answer:

Explanation:

The -intercept is the value when y=0 .

Therefore, since the two -intercepts are and , the points are (4,0) and (6,0) .

Write the slope formula, plug in the values, and solve.

$m=\frac{y_2-y_1}{x_2-x_1} = \frac{0-0}{6-4}= \frac{0}{2} =0$

The slope is zero.

Report an Error

Example Question #1 : How To Find The Slope Of A Line

Given the points (4, 3) and (8, 9) , find the slope of the line.

Possible Answers:

$\frac{-3}{4}$

$\frac{2}{3}$

$\frac{3}{2}$

$\frac{-6}{4}$

$\frac{4}{3}$

Correct answer:

$\frac{3}{2}$

Explanation:

The formula for the slope of a line is $\frac{y_2-y_1}{x_2-x_1}$ .

We then plug in the points given: $\frac{9-3}{8-4}=\frac{6}{4}$ which is then reduced to $\frac{3}{2}$ .

Report an Error

Example Question #2 : Graph Proportional Relationships, Interpreting The Unit Rate As The Slope: Ccss.Math.Content.8.Ee.B.5

A line crosses the x-axis at (6,8) and the y-axis at (0,6) . What is the slope of this line?

Possible Answers:

None of these.

m=3

$m=-\frac{1}{3}$

m=-3

$m=\frac{1}{3}$

Correct answer:

$m=\frac{1}{3}$

Explanation:

Given the points,

$\\(x_1,y_1)=(0,6) \\(x_2,y_2)=(6,8)$ .

We compute slope (m) as follows:

$m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{8-6}{6-0}=\mathbf{\frac{1}{3}}$

Report an Error

Example Question #1423 : Intermediate Geometry

Find the slope of the line that passes through the points:

(12, 2) and (-12, 4)

Possible Answers:

$-\frac{3}{4}$

$-\frac{1}{12}$

Correct answer:

$-\frac{1}{12}$

Explanation:

Recall that the slope of a line also measures how steep the line is. Use the following equation to find the slope of the line:

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$

Now, substitute in the information using the given points.

$\text{Slope}=\frac{4-2}{-12-12}$

Simplify.

$\text{Slope}=\frac{2}{-24}$

Solve.

$\text{Slope}=-\frac{1}{12}$

Report an Error

Example Question #1424 : Intermediate Geometry

Find the slope of the line that passes through the points:

(2, 4) and (-10, -20)

Possible Answers:

$-\frac{1}{2}$

$\frac{7}{8}$

Correct answer:

Explanation:

Recall that the slope of a line also measures how steep the line is. Use the following equation to find the slope of the line:

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$

Now, substitute in the information using the given points.

$\text{Slope}=\frac{-20-4}{-10-2}$

Simplify.

$\text{Slope}=\frac{-24}{-12}$

Solve.

$\text{Slope}=2$

Report an Error

Example Question #2 : How To Find The Slope Of A Line

Find the slope of the line that passes through the points:

(4, 5) and (-3, 1)

Possible Answers:

$-\frac{2}{7}$

$\frac{4}{7}$

$\frac{3}{7}$

$\frac{5}{7}$

Correct answer:

$\frac{4}{7}$

Explanation:

Recall that the slope of a line also measures how steep the line is. Use the following equation to find the slope of the line:

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$

Now, substitute in the information using the given points.

$\text{Slope}=\frac{1-5}{-3-4}$

Simplify.

$\text{Slope}=\frac{-4}{-7}$

Solve.

$\text{Slope}=\frac{4}{7}$

Report an Error

View Tutors

Maya
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Animation and Special Effects.

View Tutors

Alex
Certified Tutor

Vanderbilt University, Bachelor of Science, Psychology. Boston University, Master of Science, Speech-Language Pathology.

View Tutors

Michelle
Certified Tutor

University of Rhode Island, Bachelor of Science, Marine Biology. University of Rhode Island, Master of Arts, High School Teac...

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Phoenix, Biology Tutors in Phoenix, GRE Tutors in Chicago, Biology Tutors in San Diego, Spanish Tutors in Chicago, Physics Tutors in Miami, French Tutors in Phoenix, English Tutors in Miami, Biology Tutors in Atlanta, GRE Tutors in Miami

Popular Courses & Classes

GRE Courses & Classes in San Diego, SAT Courses & Classes in Denver, MCAT Courses & Classes in Seattle, ACT Courses & Classes in Denver, ACT Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in Boston, MCAT Courses & Classes in Philadelphia, Spanish Courses & Classes in Chicago, GRE Courses & Classes in Washington DC, GMAT Courses & Classes in Denver

Popular Test Prep

ACT Test Prep in San Francisco-Bay Area, SSAT Test Prep in Los Angeles, LSAT Test Prep in San Francisco-Bay Area, ACT Test Prep in Phoenix, ACT Test Prep in Philadelphia, SSAT Test Prep in Washington DC, GRE Test Prep in Los Angeles, SSAT Test Prep in Denver, GMAT Test Prep in Los Angeles, ISEE Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : Other Lines

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #35 : How To Find The Equation Of A Line

Example Question #63 : Expressions & Equations

Example Question #1 : Graph Proportional Relationships, Interpreting The Unit Rate As The Slope: Ccss.Math.Content.8.Ee.B.5

Example Question #2 : Graph Proportional Relationships, Interpreting The Unit Rate As The Slope: Ccss.Math.Content.8.Ee.B.5

Example Question #66 : Expressions & Equations

Example Question #1 : How To Find The Slope Of A Line

Example Question #2 : Graph Proportional Relationships, Interpreting The Unit Rate As The Slope: Ccss.Math.Content.8.Ee.B.5

Example Question #1423 : Intermediate Geometry

Example Question #1424 : Intermediate Geometry

Example Question #2 : How To Find The Slope Of A Line

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: