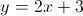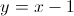All Intermediate Geometry Resources
Example Questions
Example Question #21 : Other Lines
Which of the following points is on the line ?
Start by rewriting the equation into slope-intercept form.
To find which point is on the line, take the -coordinate, and plug it into the given equation to solve for . If the -value matches the -coordinate of the same point, then the point is on the line.
Plugging in into the given equation will give the following:
Thus, is on the line.
Example Question #1372 : Intermediate Geometry
Which of the following points is on the line ?
Start by rewriting the equation into slope-intercept form.
To find which point is on the line, take the -coordinate, and plug it into the given equation to solve for . If the -value matches the -coordinate of the same point, then the point is on the line.
Plugging in into the given equation will give the following:
Thus, is on the line.
Example Question #1373 : Intermediate Geometry
Which of the following points is found on the line ?
Start by rewriting the equation into slope-intercept form.
To find which point is on the line, take the -coordinate, and plug it into the given equation to solve for . If the -value matches the -coordinate of the same point, then the point is on the line.
Plugging in into the given equation will give the following:
Thus, is on the line.
Example Question #21 : Other Lines
True or false:
The line of the equation passes through the point with coordinates .
False
True
False
A line of an equation passes through the point with coordinates if and only if, when , the equation is true. Substitute for and :
- this is false.
The line does not pass through the point.
Example Question #1382 : Intermediate Geometry
True or false:
The line of the equation passes through the origin.
True
False
True
The coordinates of the origin are , so the line of an equation passes through this point of and only if is a solution of the equation - or, equivalently, if and only if setting and makes the equation a true statement. Substitute both values:
The statement is true, so the line does pass through the origin.
Example Question #24 : How To Find Out If A Point Is On A Line With An Equation
True or false:
The lines of the equations
and
intersect at the point .
(Note: You are given that the lines are distinct)
False
True
False
If two distinct lines intersect at the point - that is, if both pass through this point - it follows that is a solution of the equations of both. Therefore, set in the equations and determine whether they are true or not.
Examine the second equation:
False; is not on the line of this equation.
Therefore, the lines cannot intersect at .
Example Question #1 : How To Find The Equation Of A Line
Given two points and , find the equation for the line connecting those two points in slope-intercept form.
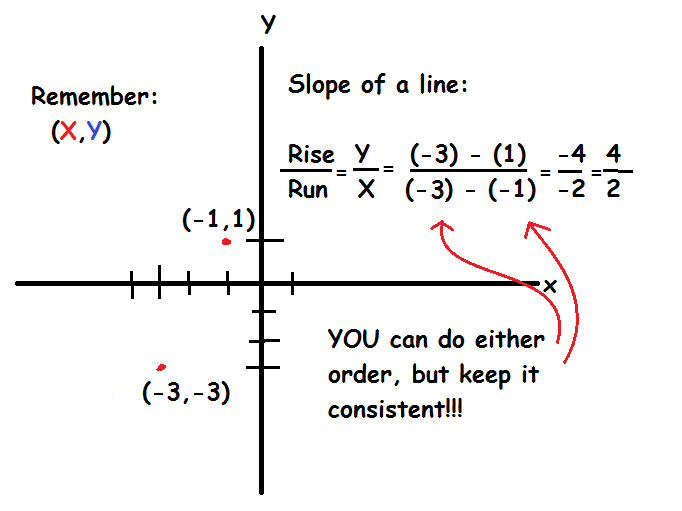
If we have two points, we can find the slope of the line between them by using the definition of the slope:
where the triangle is the greek letter 'Delta', and is used as a symbol for 'difference' or 'change in'
Now that we have our slope ( , simplified to ), we can write the equation for slope-intercept form:
where is the slope and is the y-intercept
In order to find the y-intercept, we simply plug in one of the points on our line
So our equation looks like
Example Question #2 : How To Find The Equation Of A Line
Which of the following is an equation for a line with a slope of and a y-intercept of ?
Because we have the desired slope and the y-intercept, we can easily write this as an equation in slope-intercept form (y=mx+b).
This gives us . Because this does not match either of the answers in this form (y=mx+b), we must solve the equation for x. Adding 5 to each side gives us . We can then multiple both sides by 3 and divide both sides by 4, giving us .
Example Question #3 : How To Find The Equation Of A Line
If the -intercept of a line is , and the -intercept is , what is the equation of this line?
If the y-intercept of a line is , then the -value is when is zero. Write the point:
If the -intercept of a line is , then the -value is when is zero. Write the point:
Use the following formula for slope and the two points to determine the slope:
Use the slope intercept form and one of the points, suppose , to find the equation of the line by substituting in the values of the point and solving for , the -intercept.
Therefore, the equation of this line is .
Example Question #4 : How To Find The Equation Of A Line
What is the equation of a line that has a slope of and a -intercept of ?
The slope intercept form can be written as:
where is the slope and is the y-intercept. Plug in the values of the slope and -intercept into the equation.
The correct answer is:
All Intermediate Geometry Resources