Call Now to Set Up Tutoring:

(888) 888-0446

HSPT Math : HSPT Mathematics

Study concepts, example questions & explanations for HSPT Math

Create An Account

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Rectangles

A rectangle has a width of 2x. If the length is five more than 150% of the width, what is the perimeter of the rectangle?

Possible Answers:

10(x + 1)

6x² + 5

5x + 10

6x² + 10x

5x + 5

Correct answer:

10(x + 1)

Explanation:

Given that w = 2x and l = 1.5w + 5, a substitution will show that l = 1.5(2x) + 5 = 3x + 5.

P = 2w + 2l = 2(2x) + 2(3x + 5) = 4x + 6x + 10 = 10x + 10 = 10(x + 1)

Report an Error

Example Question #2 : Quadrilaterals

ABCD is a parallelogram. BD = 5. The angles of triangle ABD are all equal. What is the perimeter of the parallelogram?

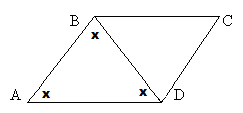
Figure_1

Possible Answers:

$10\sqrt{3}$

$15\sqrt{3}$

$11\sqrt{2}$

Correct answer:

Explanation:

If all of the angles in triangle ABD are equal and line BD divides the parallelogram, then all angles in triangle BDC must be equal as well.

We now have two equilateral triangles, so all sides of the triangles will be equal.

All sides therefore equal 5.

5+5+5+5 = 20

Report an Error

Example Question #1311 : Concepts

A square has a length of $19\textup{ feet}$ . What is the perimeter in inches?

Possible Answers:

$67\textup{ inches}$

$912\textup{ inches}$

$894\textup{ inches}$

$76\textup{ inches}$

$\frac{19}{3}\textup{ inches}$

Correct answer:

$912\textup{ inches}$

Explanation:

The square perimeter is $\textup{4 times}$ the side length.

P=4s

Substitute and multiply to find the perimeter.

$P=4(19\textup{ feet})= 76 \textup{ feet}$

There are $\textup{12 inches}$ in $\textup{1 foot}$

Multiply the perimeter with .

$76 \textup{ feet} (\frac{12 \textup{ inches}}{1 \textup{ foot}}) = 912 \textup{ inches}$

Report an Error

Example Question #131 : Quadrilaterals

Rectangle

Give the perimeter of the above rectangle in centimeters, using the conversion factor 91.44 centimeters per yard.

Possible Answers:

$1,097.28 \textrm{ cm}$

$2,194.56 \textrm{ cm}$

$2,011.68 \textrm{ cm}$

$4,389.12 \textrm{ cm}$

$1,005.84 \textrm{ cm}$

Correct answer:

$2,011.68 \textrm{ cm}$

Explanation:

The perimeter of the rectangle is 8 + 3 + 8 + 3 = 22 yards. To convert this to centimeters, multiply by the given conversion factor:

$91.44 \times 22 = 2,011.68$ centimeters.

Report an Error

Example Question #1321 : Concepts

Find the perimeter of a rectange with length 9 and width 4.

Possible Answers:

Correct answer:

Explanation:

To solve, simply use the formula for the perimeter of a rectangle.

Given the length of the rectangle is 9 and the width is 4; substitute these values into the perimeter equation.

Thus,

P=2(l+w)=2*(9+4)=2*13=26

Report an Error

Example Question #1913 : Hspt Mathematics

A square has perimeter 20. Which of the following gives 75% of the length of one of its diagonals?

Possible Answers:

$\frac{15\sqrt{3}}{4}$

$\frac{15\sqrt{2}}{4}$

$\frac{15\sqrt{3}}{2}$

$\frac{15\sqrt{2}}{2}$

Correct answer:

$\frac{15\sqrt{2}}{4}$

Explanation:

The length of one side of a square is one-fourth of its perimeter, which here makes its length

$\frac{1}{4} \cdot 20 = 5$ .

The length of a diagonal of a square is $\sqrt{2}$ times this sidelength, so the square has diagonals of length $5 \sqrt{2}$ .

75% of this is

$5 \sqrt{2} \cdot \frac{75}{100} = \frac{5 \sqrt{2}}{1} \cdot \frac{3}{4} = \frac{15 \sqrt{2}}{4}$ .

Report an Error

Example Question #1322 : Concepts

A circle has radius 8. Which of the following gives 60% of the circumference of this circle?

Possible Answers:

$\frac{192\pi }{5}$

$\frac{96 \pi }{5}$

$\frac{24 \pi }{5}$

$\frac{48 \pi }{5}$

Correct answer:

$\frac{48 \pi }{5}$

Explanation:

The circumference of a circle is its radius mulitplied by $2 \pi$ . The radius is 8, so the circumference is

$8 \cdot 2 \pi = 16 \pi$ .

60% of this is

$16 \pi \cdot \frac{60}{100}= 16 \pi \cdot \frac{3}{5} = \frac{48 \pi }{5}$

Report an Error

Example Question #1323 : Concepts

Rectangle 2

Note: Figure NOT drawn to scale.

The above rectangle has area 18. Give its perimeter.

Possible Answers:

$47\frac{15}{16}$

$17\frac{15}{26}$

$8\frac{41}{52}$

$18\frac{11}{16}$

Correct answer:

$17\frac{15}{26}$

Explanation:

The product of the length and the width of a rectangle is its area, so to find the length, divide the area by the width:

$L = A \div W = 18 \div 3\frac{1}{4} = \frac{18}{1} \div \frac{13}{4} = \frac{18}{1} \cdot \frac{4} {13} = \frac{72}{13}$

We can use $L = \frac{72}{13}$ and $W = 3\frac{1}{4} = \frac{13}{4}$ to find the perimeter by adding each of these twice:

$P = \frac{72}{13} + \frac{13}{4} + \frac{72}{13} + \frac{13}{4}$

$P = \frac{288}{52} + \frac{169}{52} +\frac{288}{52} + \frac{169}{52}$

$P = \frac{914}{52} = \frac{457}{26} = 17\frac{15}{26}$

Report an Error

Example Question #1324 : Concepts

A circle has area $\frac{16 }{25}\pi$ . Give its circumference.

Possible Answers:

$\frac{8}{5} \pi$

$\frac{64}{625} \pi$

$\frac{4}{5} \pi$

$\frac{256}{625} \pi$

Correct answer:

$\frac{8}{5} \pi$

Explanation:

The area of a circle, given its radius , is

$A = \pi r^{2}$

Set $A = \frac{16 }{25}\pi$ to find the radius.

$\frac{16 }{25}\pi = \pi r^{2}$

$\frac{16 }{25}\pi \div \pi = \pi r^{2} \div \pi$

$\frac{16 }{25} = r^{2}$

$r = \sqrt{\frac{16}{25}} = \frac{\sqrt{16}}{\sqrt{25}} = \frac{4}{5}$

Multiply this radius by $2 \pi$ to find the circumference:

$\frac{4}{5} \cdot 2 \pi = \frac{8}{5} \pi$

Report an Error

Example Question #1325 : Concepts

Rectangle 2

The above rectangle has area 100. Give its perimeter in terms of .

Possible Answers:

$2N + \frac{200}{N}$

$100 N - N^{2}$

$50 N - N^{2}$

$N + \frac{100}{N}$

Correct answer:

$2N + \frac{200}{N}$

Explanation:

The width of a rectangle is the quotient of its area and its length, which are 100 and , respectively. Therefore, the width is $\frac{100}{N}$ . The four sides measure , , $\frac{100}{N}$ , and $\frac{100}{N}$ ; the perimeter is their sum, which is

$N + N + \frac{100}{N} + \frac{100}{N} = 2N + \frac{200}{N}$

Report an Error

View Tutors

Sharon
Certified Tutor

Tabor College, Bachelor of Science, Mathematics Teacher Education. Tabor College, Masters in Education, Education.

View Tutors

Kara
Certified Tutor

University of Central Missouri, Bachelor of Science, Science Teacher Education. University of Central Missouri, Certificate, ...

View Tutors

Robert
Certified Tutor

University of North Carolina at Chapel Hill, Bachelor in Arts, English. North Carolina Central University, Master of Arts, En...

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Statistics Tutors in Boston, Reading Tutors in Chicago, Reading Tutors in New York City, English Tutors in Philadelphia, Statistics Tutors in Phoenix, Math Tutors in Philadelphia, Spanish Tutors in Houston, Chemistry Tutors in San Diego, Calculus Tutors in Houston, Physics Tutors in Miami

Popular Courses & Classes

LSAT Courses & Classes in San Diego, ISEE Courses & Classes in Philadelphia, MCAT Courses & Classes in Phoenix, ISEE Courses & Classes in Los Angeles, SSAT Courses & Classes in Seattle, GRE Courses & Classes in Chicago, ISEE Courses & Classes in Seattle, MCAT Courses & Classes in Boston, SAT Courses & Classes in Boston, SAT Courses & Classes in San Francisco-Bay Area

Popular Test Prep

ACT Test Prep in Miami, SAT Test Prep in Houston, GMAT Test Prep in Denver, GRE Test Prep in Chicago, SSAT Test Prep in Denver, GMAT Test Prep in New York City, ACT Test Prep in Phoenix, ISEE Test Prep in Boston, ISEE Test Prep in Philadelphia, SAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

HSPT Math : HSPT Mathematics

Study concepts, example questions & explanations for HSPT Math

All HSPT Math Resources

Example Questions

Example Question #1 : Rectangles

Example Question #2 : Quadrilaterals

Example Question #1311 : Concepts

Example Question #131 : Quadrilaterals

Example Question #1321 : Concepts

Example Question #1913 : Hspt Mathematics

Example Question #1322 : Concepts

Example Question #1323 : Concepts

Example Question #1324 : Concepts

Example Question #1325 : Concepts

All HSPT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: