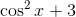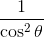Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Trigonometry

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Trigonometric Identities

Simplify:

$\sin^2x+\cos^2x+\tan^2x$

Possible Answers:

$\csc^2 x$

$\sin x\cos x$

$\sec^2x$

$2\cos x+\cot x$

This is the most simplified version.

Correct answer:

$\sec^2x$

Explanation:

Whenever you see a trigonometric function squared, start looking for a Pythagorean identity.

The two identities used in this problem are $\sin^2 x + \cos ^2 x=1$ and $\tan^2 x +1 =\sec^2 x$ .

Substitute and solve.

$\sin^2x+\cos^2x+\tan^2x=?$

$(\sin^2x+\cos^2x)+\tan^2x=?$

$(1)+\tan^2x=\sec^2 x$

Report an Error

Example Question #1 : Using Identities Of Squared Functions

Factor and simplify 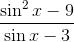$\frac{\sin^2x-9}{\sin x-3}$ .

Possible Answers:

$\cos^2 x+3$

$\sin x \cos x$

$\csc x$

This is already it's most reduced form.

$\sin x+3$

Correct answer:

$\sin x+3$

Explanation:

To reduce 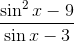$\frac{\sin^2x-9}{\sin x-3}$ , factor the numerator: $\frac{(\sin x-3)(\sin x+3)}{\sin x-3}$

Notice that we can cancel out a $\sin x -3$ .

This leaves us with 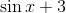$\sin x +3$ .

Report an Error

Example Question #4 : Trigonometric Identities

Simplify $\sin x\cot x$ .

Possible Answers:

$\tan x$

$\csc x$

$cos \, x$

$\cos^2x$

$\sin x \cos x$

Correct answer:

$cos \, x$

Explanation:

To simplify $\sin x\cot x$ , break them into their SOHCAHTOA parts:

$\frac{\text{opposite}}{\text{hypotenuse}}*\frac{\text{adjacent}}{\text{opposite}}$ .

Notice that the opposite's cancel out, leaving $\frac{\text{adjacent}}{\text{hypotenuse}}=\cos x$ .

Report an Error

Example Question #11 : Trigonometric Identities

Simplify $\csc x \tan x$ .

Possible Answers:

$\sin x \cos x$

This is the most simplified version.

$\cos x$

$\sec x$

Correct answer:

$\sec x$

Explanation:

Break down $\csc x \tan x$ into SOHCAHTOA to solve:

$\csc=\frac{\text{hypotenuse}}{\text{opposite}}$ and $\tan=\frac{\text{opposite}}{\text{adjacent}}$ .

Therefore, $\csc x \tan x=\frac{\text{hypotenuse}}{\text{opposite}}*\frac{\text{opposite}}{\text{adjacent}}$ . Note that the opposite's cancel out, leaving $\frac{\text{hypotenuse}}{\text{adjacent}}$ , which is the same as $\sec x$ .

Report an Error

Example Question #1 : Using Identities Of Inverse Operations

$\textup{Which of the following expressions is equal to }\frac{\tan \theta }{\sec \theta }\:\textup{?}$

Possible Answers:

$\csc\theta$

$\cot\theta$

$\cos\theta$

$\sin\theta$

$\frac{1}{\cos ^{2}\theta }$

Correct answer:

$\sin\theta$

Explanation:

$\textup{Use identities to solve: }\tan\theta=\frac{\sin \theta }{\cos \theta }\:\:\:\:\:\sec\theta=\frac{1}{\cos \theta }$

$\frac{\tan \theta }{\sec \theta }=\frac{\sin \theta }{\cos \theta }\times\frac{\cos \theta }{1}=\sin\theta$

Report an Error

View Tutors

Daniella
Certified Tutor

Harvard University, Bachelor of Science, Applied Mathematics.

View Tutors

Dinesh
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Computer Science.

View Tutors

Raymond
Certified Tutor

Western Washington University, Bachelor in Arts, Foreign Languages and Literatures, General.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Reading Tutors in Dallas Fort Worth, MCAT Tutors in San Francisco-Bay Area, Computer Science Tutors in Chicago, Reading Tutors in Philadelphia, English Tutors in Boston, Spanish Tutors in San Francisco-Bay Area, MCAT Tutors in Denver, GRE Tutors in Phoenix, MCAT Tutors in Seattle, Chemistry Tutors in Boston

Popular Courses & Classes

ISEE Courses & Classes in Boston, ISEE Courses & Classes in Miami, ACT Courses & Classes in Denver, ACT Courses & Classes in Miami, GRE Courses & Classes in Chicago, Spanish Courses & Classes in Philadelphia, LSAT Courses & Classes in Boston, ISEE Courses & Classes in Denver, GMAT Courses & Classes in Phoenix, GRE Courses & Classes in Boston

Popular Test Prep

SSAT Test Prep in Denver, MCAT Test Prep in New York City, SAT Test Prep in San Diego, ISEE Test Prep in Chicago, LSAT Test Prep in San Diego, ACT Test Prep in Miami, ISEE Test Prep in Boston, SAT Test Prep in Miami, LSAT Test Prep in Chicago, LSAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Trigonometry

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : Trigonometric Identities

Example Question #1 : Using Identities Of Squared Functions

Example Question #4 : Trigonometric Identities

Example Question #11 : Trigonometric Identities

Example Question #1 : Using Identities Of Inverse Operations

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: