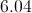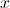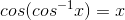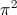Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Trigonometry

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Graphing The Sine And Cosine Functions

Trig_id

If $\theta$ equals $55^{\circ}$ and is 15ft , how long is ?

Possible Answers:

8.6ft

13.2ft

Not enough information to solve

12.3ft

11.3ft

Correct answer:

12.3ft

Explanation:

This problem can be easily solved using trig identities. We are given the hypotenuse (15ft) and $\theta (55^{\circ})$ . We can then calculate side using the $\sin$ .

$\sin=\frac{opposite}{hypotenuse}$

$\sin55^{\circ}=\frac{o}{15ft}$

Rearrange to solve for .

$o=\sin55^{\circ}*15ft$

$\dpi{100} \rightarrow 12.3ft$

If you calculated the side to equal 8.6ft then you utilized the $\cos$ function rather than the $\sin$ .

Report an Error

Example Question #4 : Finding Sides

Triangle

What is the length of CB?

Possible Answers:

$\frac{AB}{\sin A}$

$\frac{\tan C}{AB}$

$\frac{\sin B}{AC}$

$\frac{AB}{\tan C}$

$\frac{AC}{\sin A}$

Correct answer:

$\frac{AB}{\tan C}$

Explanation:

$\tan X= \frac{OPPOSITE}{ADJACENT}$

$\tan C=\frac{AB}{CB}$

$CB= \frac{AB}{\tan C}$

Report an Error

Example Question #1 : Trigonometric Equations

If $tanx=\frac{1}{3}$ , find $f(x)=\frac{sin(3\pi +x)+sin(x-\frac{\pi }{2})}{cos(x-\pi )+cos(\frac{3\pi }{2}+x)}$ .

Possible Answers:

-2

-1

Correct answer:

Explanation:

First we need to simplify each term:

$sin(3\pi +x)= -sinx$

$sin(x-\frac{\pi }{2})=cosx$

$cos(x-\pi )=- cosx$

$cos(\frac{3\pi }{2}+x)=sinx$

So we will have:

$f(x)=\frac{-sinx-cosx}{-cosx+sinx}$

Since we have the value of tanx , we can divide the numerator and denominator by cosx .

$f(x)=\frac{-\frac{sinx}{cosx}-\frac{cosx}{cosx}}{\frac{-cosx}{cosx}+\frac{sinx}{cosx}}=\frac{-tanx-1}{-1+tanx} = \frac{1+tanx}{1-tanx}$

We can then substitute the value of tanx in the obtained function.

$f(x)=\frac{1+\frac{1}{3}}{1-\frac{1}{3}}=\frac{\frac{4}{3}}{\frac{2}{3}}=2$

Report an Error

Example Question #2 : Solving Trigonometric Equations

A right triangle has an angle of $41^\circ$ . If the side opposite it has a length of , what is the hypotenuse?

Possible Answers:

6.04

9.2

5.25

10.6

12.19

Correct answer:

12.19

Explanation:

For this problem we will use the sine function as $\sin=\frac{O}{H}$ .

Plug in our given information:

$\sin(41^\circ)=\frac{8}{H}$

$H=\frac{8}{\sin(41^\circ)}$

H=12.19

Report an Error

Example Question #3 : Solving Trigonometric Equations

A right triangle has an angle of $72^\circ$ . If the side adjacent to it has a length of , what is the hypotenuse?

Possible Answers:

3.4

35.6

10.46

11.56

3.57

Correct answer:

35.6

Explanation:

For this problem we will use the cosine function as $\cos=\frac{A}{H}$ .

Plug in our given information:

$\cos(72^\circ)=\frac{11}{H}$

$H=\frac{11}{\cos(72^\circ)}$

H=35.6

Report an Error

Example Question #1 : Solving Trigonometric Equations

In a right triangle, if

$cos(x)=\frac{3}{5}$

and

$cos(y)=\frac{4}{5}$

then what does $\tan(x)$ equal?

Possible Answers:

$\frac{3}{5}$

$\frac{3}{4}$

$\frac{5}{4}$

$\frac{4}{3}$

Correct answer:

$\frac{4}{3}$

Explanation:

One can draw a right triangle with acute angles $\angle x$ and $\angle y$ . The side adjacent to $\angle y$ is 4, and the side adjacent to $\angle x$ is 3.

$tan(x)=\frac{opposite}{adjacent}$

Report an Error

Example Question #1 : Trigonometric Equations

If $sinx-cosx=\frac{1}{3}$ , find the value of the function $f(x)=sin^{3}x+cos^{3}x$ .

Possible Answers:

$\frac{13}{27}$

$-\frac{13}{27}$

$\frac{11}{27}$

$-\frac{11}{27}$

Correct answer:

$\frac{13}{27}$

Explanation:

We can write:

$sinx-cosx=\frac{1}{3}$

$\Rightarrow (sinx-cosx)^{2}=\frac{1}{9}$

$\Rightarrow sin^2x+cos^2x-2sinxcosx=\frac{1}{9}$

$\Rightarrow 2sinxcosx=1-\frac{1}{9}$

$\Rightarrow sinxcosx=\frac{4}{9}$

We can also write:

(sinx-cosx)^3=sin^3x+cos^3x+3sinxcos^2x-3cosxsin^2x

$\Rightarrow sin^3x+cos^3x=(sinx-cosx)^3+3sinxcosx(sinx-cosx)$

Now we can substitute the values of (sinx - cosx) and (sinx * cosx) in the obtained function:

$\Rightarrow sin^3x+cos^3x=(\frac{1}{3})^3+3*\frac{4}{9}*\frac{1}{3}=\frac{1}{27}+\frac{4}{9}=\frac{13}{27}$

Report an Error

Example Question #72 : Pre Calculus

Which of the following is not in the range of the function $y = \sin{x}$ ?

Possible Answers:

$\frac{3}{4}$

$\frac{2}{3}$

$-\frac{1}{2}$

$\frac{3}{2}$

Correct answer:

$\frac{3}{2}$

Explanation:

The range of the function $y= \sin x$ is all numbers between and (the sine wave never goes above or below this).

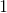
Of the choices given, $\frac{3}{2}$ is greater than and thus not in this range.

Report an Error

Example Question #1 : Trigonometric Functions And Graphs

Simplify the function below:

$f(x)=cos^2(\frac{1}{2}cos^{-1}x)$

Possible Answers:

cosx

$\frac{1-x}{2}$

$\frac{1+x}{2}$

$\frac{x}{2}$

Correct answer:

$\frac{1+x}{2}$

Explanation:

We need to use the following formulas:

a) $cos^2x=\frac{1+cos2x}{2}$

and

b) $cos(cos^{-1}x)=x$

We can simplify f(x) as follows:

$f(x)=cos^2(\frac{1}{2}cos^{-1}x)=\frac{1+cos(cos^{-1}x)}{2}=\frac{1+x}{2}$

Report an Error

Example Question #1 : Understanding Period And Amplitude

What is the period of

$\tan \left ( \frac{x}{\pi } \right )$ ?

Possible Answers:

$\pi^{2}$

$\frac{1}{\pi }$

$\pi$

$2\pi$

Correct answer:

$\pi^{2}$

Explanation:

The period for $\tan(x)$ is $\pi$ . However, if a number is multiplied by , you divide the period $\pi$ by what is being multiplied by . Here, $(1/\pi )$ is being multiplied by . $\pi/(1/\pi )$ equals $\pi^{2}$ .

Report an Error

View Tutors

Claryse
Certified Tutor

St. Mary's University, Bachelor of Education, Education.

View Tutors

Mohammed
Certified Tutor

University of Maryland-College Park, Bachelor of Science, Electrical Engineering. University of Maryland-College Park, Master...

View Tutors

Yewande
Certified Tutor

Ryerson University, Master of Laws, Prelaw Studies.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

LSAT Tutors in Washington DC, Calculus Tutors in Miami, Chemistry Tutors in Los Angeles, Computer Science Tutors in Denver, Computer Science Tutors in Phoenix, SSAT Tutors in Seattle, Physics Tutors in Boston, Physics Tutors in Houston, Reading Tutors in Miami, English Tutors in Houston

Popular Courses & Classes

SSAT Courses & Classes in Chicago, GMAT Courses & Classes in Washington DC, GRE Courses & Classes in Seattle, GRE Courses & Classes in Atlanta, SAT Courses & Classes in Denver, ISEE Courses & Classes in Philadelphia, ACT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Phoenix, SAT Courses & Classes in Philadelphia, GMAT Courses & Classes in Houston

Popular Test Prep

SSAT Test Prep in Dallas Fort Worth, LSAT Test Prep in Miami, GMAT Test Prep in Phoenix, GMAT Test Prep in Houston, ISEE Test Prep in San Diego, ISEE Test Prep in Washington DC, MCAT Test Prep in Miami, ISEE Test Prep in Los Angeles, GRE Test Prep in San Francisco-Bay Area, GRE Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Trigonometry

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : Graphing The Sine And Cosine Functions

Example Question #4 : Finding Sides

Example Question #1 : Trigonometric Equations

Example Question #2 : Solving Trigonometric Equations

Example Question #3 : Solving Trigonometric Equations

Example Question #1 : Solving Trigonometric Equations

Example Question #1 : Trigonometric Equations

Example Question #72 : Pre Calculus

Example Question #1 : Trigonometric Functions And Graphs

Example Question #1 : Understanding Period And Amplitude

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: