Obtain the radius of the circle from the area.

Split the square up into 4 triangles by connecting opposite corners. These triangles will have a right angle at the center of the square, formed by two radii of the circle, and two 45-degree angles at the square's corners. Because you have a 45-45-90 triangle, you can calculate the sides of the triangles to be , , and . The radii of the circle (from the center to the corners of the square) will be 9. The hypotenuse (side of the square) must be .

The area of the square is then .

For the circle to contain all 3 vertices, the hypotenuse must be the diameter of the circle. The hypotenuse, and therefore the diameter, is 5, since this must be a 3-4-5 right triangle.

The equation for the area of a circle is A = πr².

To find the ratio we must know the equation for the circumference of a circle. In this equation, is the circumference and is the diameter.

Once we know the equation, we can solve for the ratio of the diameter to circumference by solving the equation for . We do this by dividing both sides by .

Then we divide both sides by the circumference.

We now know that the ratio of the diameter to circumference is equal to .

To find the ratio we must know the equation for the circumference of a circle is

Once we know the equation we can solve for the ratio of the diameter to circumference by solving the equation for 

we divide both sides by the circumference giving us 

We now know that the ratio of the diameter to circumference is equal to .

The formula for the area of a circle is , and the formula for circumference is . If we solve for C in terms of r, we get
.

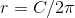
We can then substitute this value of r into the formula for the area:

The circumference of any circle is 

So the ratio of its circumference to its radius r, is

The distance between each notch on the clock is 6 degrees because there are 360 degrees on the clock, and there are 60 notches total. The minute hand is at notch #20, and so it is 120 degrees from the top. The hour hand is a little past notch #40 because the time is a little past hour 8. Thus, the hour hand is a little past 240 degrees from the top, going clockwise ( degrees).

In each hour, the hour hand goes 5 notches, or 30 degrees.  Because it is now 20 minutes past the hour, a third of an hour has passed.  One third of 30 degrees is 10 degrees.  Thus, the hour hand is 10 degrees past notch #40.  The hour hand is 250 degrees from the top, going clockwise.  The angle between the two hands is thus 130 degrees.  

This is a proportion problem

  so there are  in  percent of a circle

First note that a clock is a circle made of 360 degrees, and that each number represents an angle and the separation between them is 360/12 = 30. And at 2:00, the minute hand is on the 12 and the hour hand is on the 2.  The correct answer is 2 * 30 = 60 degrees.

The interior angle of a sector is equal the the angle of the sector. If the entire circumference was the sector, it would equal . Additionally, if it were 12:00, the angle would be equal to . We can solve the problem by setting up a proportion. 2:00 will be two-twelfths of the circle past the 12:00 mark, and will be at an angle of .

Cross multiply and solve for .