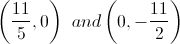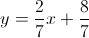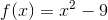We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : Understanding Vertical And Horizontal Lines

Which of the following is a vertical line?

Possible Answers:

y = 3x + 2

$y = \frac{1}{x}$

y = x

y = 4

x = 3

Correct answer:

x = 3

Explanation:

A vertical line is one in which the values can vary. Namely, there is only one possible value for , and can be any number. Thus, by this description, the only vertical line listed is x = 3 .

Report an Error

Example Question #2 : Understanding Vertical And Horizontal Lines

Which of the following has a slope of 0?

Possible Answers:

$y = 3^{x}$

x = 0

y = x

y = 10

$y = \frac{1}{x}$

Correct answer:

y = 10

Explanation:

A line with a slope of zero will be horizontal. A horizontal line has only one possible value for , and can be any value.

Thus, the only given equation which fits this description is y = 10 .

Report an Error

Example Question #812 : Algebra Ii

Which of the following is a vertical line?

Possible Answers:

x = 2

y = 3x + 3

y = -x + 2

y = 0

y = 6

Correct answer:

x = 2

Explanation:

A vertical line has infinitely many values of but only one value of . Thus, vertical lines are of the form x = c , where is a real number. The only equation of this form is x = 2 .

Report an Error

Example Question #1671 : High School Math

Solve for the - and - intercepts:

5x-2y=11

Possible Answers:

$\left ( -\frac{11}{5},0\right)\ and \left ( 0,-\frac{11}{2}\right)$

$\left ( -\frac{11}{5},0\right)\ and \left ( 0,\frac{11}{2}\right)$

$\left ( \frac{11}{5},0\right)\ and \left ( 0,\frac{11}{2}\right)$

$\left ( \frac{11}{5},0\right)\ and \left ( 0,-\frac{11}{2}\right)$

Correct answer:

$\left ( \frac{11}{5},0\right)\ and \left ( 0,-\frac{11}{2}\right)$

Explanation:

To solve for the -intercept, set to zero and solve for :

5x-2y=11

5x-2(0)=11

5x=11

$x=\frac{11}{5}$

To solve for the -intercept, set to zero and solve for :

5x-2y=11

5(0)-2y=11

-2y=11

$y=-\frac{11}{2}$

Report an Error

Example Question #1672 : High School Math

Solve:

x+3y=10

-2x+y=1

Possible Answers:

(3,-2)

Infinitely many solutions

(-2,1)

No solutions

(1,3)

Correct answer:

(1,3)

Explanation:

Use substution to solve this problem:

x+3y=10 becomes x=10-3y and then is substituted into the second equation. Then solve for :

-2(10-3y)+y=1 , so y=3 and x=1 to give the solution (1,3) .

Report an Error

Example Question #1673 : High School Math

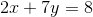
Write 2x+7y=8 in slope-intercept form.

Possible Answers:

$y=\frac{2}{7}x-\frac{8}{7}$

$y=\frac{2}{7}x+\frac{8}{7}$

$y=\frac{-2}{7}x-\frac{8}{7}$

$y=\frac{-2}{7}x+\frac{8}{7}$

Correct answer:

$y=\frac{-2}{7}x+\frac{8}{7}$

Explanation:

Slope-intercept form is y=mx+b .

2x+7y=8

7y=-2x+8

$y=\frac{-2}{7}x+\frac{8}{7}$

Report an Error

Example Question #11 : Graphing Functions

Based on the figure below, which line depicts a quadratic function?

Possible Answers:

Red line

Green line

Blue line

Purple line

None of them

Correct answer:

Red line

Explanation:

A parabola is one example of a quadratic function, regardless of whether it points upwards or downwards.

The red line represents a quadratic function and will have a formula similar to $\small {f(x)=ax^2+bx+c}$ .

The blue line represents a linear function and will have a formula similar to $\small {f(x)=ax+b$ .

The green line represents an exponential function and will have a formula similar to $\small {f(x)=ax^b}$ .

The purple line represents an absolute value function and will have a formula similar to $\small {f(x)=\left |ax+b \right |}.$ .

Report an Error

Example Question #21 : Functions And Graphs

Which of the following functions represents a parabola?

Possible Answers:

$f(x) = x^{2} - 9$

$f(x) = \frac{4x^{2}}{x^{3}}$

f(x) = 5

$f(x) = x^{2} - y^{2}$

f(x) = x

Correct answer:

$f(x) = x^{2} - 9$

Explanation:

A parabola is a curve that can be represented by a quadratic equation. The only quadratic here is represented by the function $f(x) = x^{2} - 9$ , while the others represent straight lines, circles, and other curves.

Report an Error

Example Question #1 : Circle Functions

Find the radius of the circle given by the equation:

x^2+4x+y^2-12y=24

Possible Answers:

Correct answer:

Explanation:

To find the center or the radius of a circle, first put the equation in the standard form for a circle: $(x-x_{1})^2+(y-y_{1})^2=r^2$ , where is the radius and $(x_{1},y_{1})$ is the center.

From our equation, we see that it has not yet been factored, so we must do that now. We can use the formula (ax-b)^2=a^2x^2-2abx +b^2 .

a^2x^2=x^2 , so a=1 .

-2abx=4x and a=1 , so -2b=4 and b=-2 .

Therefore, x^2+4x+4=(x+2)^2 .

Because the constant, in this case 4, was not in the original equation, we need to add it to both sides:

x^2+4x+y^2-12y=24

x^2+4x+ 4+y^2-12y=24+4

(x+2)^2+y^2-12y=28

Now we do the same for :

(x+2)^2+y^2-12y+36=28+36

(x+2)^2+(y-6)^2=64

We can now find :

r^2 = 64 = 8

Report an Error

Example Question #2 : Circle Functions

Find the center of the circle given by the equation:

x^2+y^2-6x+18y=-65

Possible Answers:

$\left ( -8,5 \right )$

$\left ( 5,5 \right )$

$\left ( 6,-18 \right )$

$\left ( 3,-9 \right )$

$\left ( 12,3 \right )$

Correct answer:

$\left ( 3,-9 \right )$

Explanation:

To find the center or the radius of a circle, first put the equation in standard form: $(x-x_{1})^2+(y-y_{1})^2=r^2$ , where is the radius and $(x_{1},y_{1})$ is the center.

From our equation, we see that it has not yet been factored, so we must do that now. We can use the formula (ax-b)^2=a^2x^2-2abx +b^2 .

a^2x^2=x^2 , so a=1 .

-2abx=-6x and a=1 , so -2b=-6 and b=3 .

This gives x^2-6x+9=(x-3)^2 .

Because the constant, in this case 9, was not in the original equation, we must add it to both sides:

x^2-6x+y^2+18y=-65

x^2-6x+9+y^2+18y=-65+9

(x-3)^2+y^2+18y=-56

Now we do the same for :

(x-3)^2+y^2+18y+81=-56+81

(x-3)^2+(y+9)^2=25

We can now find the center: (3, -9)

Report an Error

View Tutors

Miguel
Certified Tutor

Miami Dade College, Bachelors, Business.

View Tutors

Tom
Certified Tutor

University of Wisconsin-Madison, Bachelor of Science, Atmospheric Sciences and Meteorology. Embry-Riddle Aeronautical Univers...

View Tutors

Tanzila
Certified Tutor

University of Virginia-Main Campus, Master of Science, Physiology.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Computer Science Tutors in Houston, SSAT Tutors in Boston, Algebra Tutors in Los Angeles, Calculus Tutors in Chicago, LSAT Tutors in Miami, Spanish Tutors in Boston, SAT Tutors in Phoenix, Statistics Tutors in Philadelphia, Computer Science Tutors in Seattle, GRE Tutors in Dallas Fort Worth

Popular Courses & Classes

LSAT Courses & Classes in New York City, LSAT Courses & Classes in Washington DC, GRE Courses & Classes in Los Angeles, ISEE Courses & Classes in Phoenix, ISEE Courses & Classes in Washington DC, GMAT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in San Diego, ISEE Courses & Classes in Seattle, ACT Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Dallas Fort Worth

Popular Test Prep

MCAT Test Prep in Miami, GMAT Test Prep in San Diego, GRE Test Prep in Atlanta, ACT Test Prep in Philadelphia, SAT Test Prep in Boston, GMAT Test Prep in Houston, GMAT Test Prep in Los Angeles, MCAT Test Prep in Dallas Fort Worth, ISEE Test Prep in Chicago, ISEE Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #2 : Understanding Vertical And Horizontal Lines

Example Question #2 : Understanding Vertical And Horizontal Lines

Example Question #812 : Algebra Ii

Example Question #1671 : High School Math

Example Question #1672 : High School Math

Example Question #1673 : High School Math

Example Question #11 : Graphing Functions

Example Question #21 : Functions And Graphs

Example Question #1 : Circle Functions

Example Question #2 : Circle Functions

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: