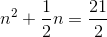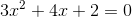We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #4 : Completing The Square

Complete the square:

2n^2+n-21=0

Possible Answers:

$n=-\frac{5}{2},3$

$n=-\frac{7}{2},3$

$n=-\frac{7}{2},4$

$n=-\frac{9}{2},3$

$n=-\frac{7}{2},2$

Correct answer:

$n=-\frac{7}{2},3$

Explanation:

Begin by dividing the equation by and adding 10.5 to each side:

2n^2+n-21=0

$n^2+\frac{1}{2}n = \frac{21}{2}$

Square the value in front of the and add to each side:

$n^2+\frac{1}{2}n + \frac{1}{16} = \frac{21}{2} + \frac{1}{16}$

Factor the left side of the equation:

$(n+\frac{1}{4})^2 = \frac{169}{16}$

Take the square root of both sides and simplify:

$n+\frac{1}{4} = \frac{\pm 13}{4}$

$n = \frac{-1 \pm 13}{4}$

$n=-\frac{7}{2},3$

Report an Error

Example Question #32 : Solving Quadratic Equations

Complete the square:

3x^2+4x+2=0

Possible Answers:

$x=\frac{-3 \pm i\sqrt{2}}{3}$

$x=\frac{-2 \pm i\sqrt{2}}{4}$

$x=\frac{-4 \pm i\sqrt{2}}{3}$

$x=\frac{-2 \pm i\sqrt{3}}{3}$

$x=\frac{-2 \pm i\sqrt{2}}{3}$

Correct answer:

$x=\frac{-2 \pm i\sqrt{2}}{3}$

Explanation:

Begin by dividing the equation by and subtracting $\frac{2}{3}$ from each side:

3x^2+4x+2=0

$x^2+\frac{4}{3}x = -\frac{2}{3}$

Square the value in front of the and add to each side:

$x^2+\frac{4}{3}x +\frac{4}{9} = -\frac{2}{3}+\frac{4}{9}$

Factor the left side of the equation:

$(x+\frac{2}{3})^2 = \frac{-2}{9}$

Take the square root of both sides and simplify:

$x+\frac{2}{3} = \frac{\pm \sqrt{-2}}{3}$

$x = \frac{-2 \pm i\sqrt{2}}{3}$

Report an Error

Example Question #341 : Algebra Ii

Solve using the quadratic formula:

2x^2+2x+3=0

Possible Answers:

$x= \frac{-1 \pm i\sqrt{5}}{3}$

$x= \frac{-2 \pm i\sqrt{5}}{3}$

$x= \frac{-1 \pm i\sqrt{5}}{2}$

$x= \frac{-3 \pm i\sqrt{5}}{2}$

$x= \frac{-2 \pm i\sqrt{5}}{2}$

Correct answer:

$x= \frac{-1 \pm i\sqrt{5}}{2}$

Explanation:

Use the quadratic formula to solve:

$x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}$

a = 2

b = 2

c = 3

$x = \frac{-(2) \pm \sqrt{(2)^2-4(2)(3)}}{2(2)}$

$x = \frac{-2 \pm \sqrt{-20}}{4}$

$x = \frac{-2 \pm 2i\sqrt{5}}{4}$

$x = \frac{-1 \pm i\sqrt{5}}{2}$

Report an Error

Example Question #91 : Intermediate Single Variable Algebra

Solve using the quadratic formula:

2a^2-5a+4=0

Possible Answers:

$a=\frac{4 \pm i\sqrt{7}}{4}$

$a=\frac{6 \pm i\sqrt{7}}{4}$

$a=\frac{3 \pm i\sqrt{7}}{4}$

$a=\frac{7 \pm i\sqrt{7}}{4}$

$a=\frac{5 \pm i\sqrt{7}}{4}$

Correct answer:

$a=\frac{5 \pm i\sqrt{7}}{4}$

Explanation:

Use the quadratic formula to solve:

$x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}$

a = 2

b = -5

c = 4

$a = \frac{-(-5) \pm \sqrt{(-5)^2-4(2)(4)}}{2(2)}$

$a = \frac{5 \pm \sqrt{-7}}{4}$

$a = \frac{5 \pm i\sqrt{7}}{4}$

Report an Error

Example Question #92 : Intermediate Single Variable Algebra

Solve using the quadratic formula:

ax^2+bx+3b=0

Possible Answers:

$x=\frac{b \pm \sqrt{b^2-12ab}}{a}$

$x=\frac{b \pm \sqrt{b^2-12ab}}{2a}$

$x=\frac{-b \pm \sqrt{b^2-8ab}}{2a}$

$x=\frac{-b \pm \sqrt{b^2-12ab}}{a}$

$x=\frac{-b \pm \sqrt{b^2-12ab}}{2a}$

Correct answer:

$x=\frac{-b \pm \sqrt{b^2-12ab}}{2a}$

Explanation:

Use the quadratic formula to solve:

$x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}$

a = a

b = b

c = 3b

$x = \frac{-(b) \pm \sqrt{(b)^2-4(a)(3b)}}{2(a)}$

$x = \frac{-b \pm \sqrt{b^2-12ab}}{2a}$

Report an Error

Example Question #93 : Intermediate Single Variable Algebra

Solve using the quadratric formula:

bx^2+acx+c=0

Possible Answers:

$x=\frac{-ac\sqrt{a^2c^2-4bc}}{2b}$

$x=\frac{-ac\sqrt{a^2c^2-4bc}}{b}$

$x=\frac{-ac\sqrt{a^2c^2-2bc}}{2b}$

$x=\frac{ac\sqrt{a^2c^2-4bc}}{b}$

$x=\frac{ac\sqrt{a^2c^2-4bc}}{2b}$

Correct answer:

$x=\frac{-ac\sqrt{a^2c^2-4bc}}{2b}$

Explanation:

Use the quadratic formula to solve:

$x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}$

a = b

b = ac

c = c

$x = \frac{-(ac) \pm \sqrt{(ac)^2-4(b)(c)}}{2(b)}$

$x = \frac{-ac \pm \sqrt{a^2c^2-4bc}}{2b}$

Report an Error

Example Question #1601 : Algebra Ii

A baseball that is thrown in the air follows a trajectory of h(t)= -4t^2 +12t+6 , where h(t) is the height of the ball in feet and is the time elapsed in seconds. How long does the ball stay in the air before it hits the ground?

Possible Answers:

Between 3.5 and 4 seconds

Between 3 and 3.5 seconds

Between 2.5 and 3 seconds

Between 4 and 4.5 seconds

Between 2 and 2.5 seconds

Correct answer:

Between 3 and 3.5 seconds

Explanation:

To solve this, we look at the equation h(t)=0 .

Setting the equation equal to 0 we get 0= -4t^2 +12t+6 .

Once in this form, we can use the Quadratic Formula to solve for .

The quadratic formula says that if 0= -ax^2 +bx+c , then

$x= \frac{-b\pm\sqrt(b^2-4ac)}{2a}$ .

Plugging in our values:

$t= \frac{-12\pm\sqrt{(12^2-4(-4)(6)}}{2(-4)}=\frac{-12\pm \sqrt{240}}{-8}= \frac{12\pm15.5}{8}$

Therefore t=3.4375 or -.4375 and since we are looking only for positive values (because we can't have negative time), 3.4375 seconds is our answer.

Report an Error

Example Question #1 : Solving Quadratic Inequalities

Solve the quadratric inequality:

$y\geq -x^2+10x-21$

Possible Answers:

$x\leq1 , x\geq4$

$x\leq5 , x\geq9$

$x\leq3 , x\geq7$

$x\leq2 , x\geq5$

$x\leq4 , x\geq8$

Correct answer:

$x\leq3 , x\geq7$

Explanation:

Factor and solve.

$y\geq -x^2+10x-21$

$y\leq x^2-10x+21$

Since the equation is less than or equal to, you know the inequality will be OR, not AND.

$y\leq (x-7)(x-3)$

$x\leq3$ or $x\geq7$

Report an Error

Example Question #2 : Solving Quadratic Inequalities

Solve the following quadratic inequality:

$y\leq x^2+4x+3$

Possible Answers:

$x\leq -2, x\geq -1$

$x\leq -4, x\geq -2$

$x\leq -3, x\geq -1$

$x\leq -4, x\geq -1$

$x\leq -3, x\geq -2$

Correct answer:

$x\leq -3, x\geq -1$

Explanation:

Factor and solve. Since the sign is less than or equal to, we know the inequality will be OR, not AND.

$y\leq x^2+4x+3$

$y\leq (x+3)(x+1)$

$x\leq-3$ or $x\geq -1$

Report an Error

Example Question #41 : Solving Quadratic Equations

Solve the following quadratic inequality:

$y\leq -x^2+6x+5$

Possible Answers:

$3-\sqrt{13}\leq x \leq 3+\sqrt{13}$

$3-\sqrt{10}\leq x \leq 3+\sqrt{10}$

$3-\sqrt{14}\leq x \leq 3+\sqrt{14}$

$3-\sqrt{15}\leq x \leq 3+\sqrt{15}$

$3-\sqrt{11}\leq x \leq 3+\sqrt{11}$

Correct answer:

$3-\sqrt{14}\leq x \leq 3+\sqrt{14}$

Explanation:

Use the quadratic formula to solve.

$y\leq -x^2+6x+5$

$y\geq x^2-6x-5$

Since the inequality is greater than or equal to, we know the inequality will be AND, not OR.

$x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}$

a=1

b=-6

c=-5

$x = \frac{-(-6) \pm \sqrt{(-6)^2-4(1)(-5)}}{2(1)}$

$x= \frac{6 \pm \sqrt{56}}{2}$

$x= 3 \pm \sqrt{14}$

$3-\sqrt{14}\leq x \leq 3+\sqrt{14}$

Report an Error

View Tutors

Mark
Certified Tutor

Eastern Michigan University, Bachelor of Science, Education of Individuals in Secondary Special Education Programs. Eastern M...

View Tutors

Kylee
Certified Tutor

DeSales University, Bachelor of Science, Biology, General. Sidney Kimmel Medical College at Thomas Jefferson University , Pro...

View Tutors

Sharif
Certified Tutor

NCCU, Bachelors, Physics and Mathematics.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Reading Tutors in Los Angeles, English Tutors in Miami, ISEE Tutors in Miami, French Tutors in Phoenix, Statistics Tutors in Seattle, SSAT Tutors in San Diego, ACT Tutors in Chicago, Chemistry Tutors in Houston, Chemistry Tutors in San Francisco-Bay Area, GMAT Tutors in Chicago

Popular Courses & Classes

MCAT Courses & Classes in New York City, SAT Courses & Classes in Denver, LSAT Courses & Classes in Washington DC, GMAT Courses & Classes in Los Angeles, ACT Courses & Classes in Denver, MCAT Courses & Classes in Miami, GRE Courses & Classes in San Diego, GRE Courses & Classes in Phoenix, ACT Courses & Classes in Seattle, Spanish Courses & Classes in New York City

Popular Test Prep

ACT Test Prep in Seattle, GMAT Test Prep in Los Angeles, SAT Test Prep in Phoenix, GRE Test Prep in Los Angeles, LSAT Test Prep in Washington DC, ACT Test Prep in Houston, SAT Test Prep in Miami, ACT Test Prep in Dallas Fort Worth, LSAT Test Prep in Dallas Fort Worth, SSAT Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : High School Math

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #4 : Completing The Square

Example Question #32 : Solving Quadratic Equations

Example Question #341 : Algebra Ii

Example Question #91 : Intermediate Single Variable Algebra

Example Question #92 : Intermediate Single Variable Algebra

Example Question #93 : Intermediate Single Variable Algebra

Example Question #1601 : Algebra Ii

Example Question #1 : Solving Quadratic Inequalities

Example Question #2 : Solving Quadratic Inequalities

Example Question #41 : Solving Quadratic Equations

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: