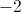Multiply the equation by :

Simplify:

We are asked to solve the equation .

Often, when solving equations involving rational expressions, it helps to elminate fractions by multiplying both sides of the equation by the denominators of each term intervolved. 

In the context of this problem, we can first multiply both sides of the equation by x+2 to eliminate the denominator of the first term.

Be sure to distribute the x+2 to each term on the left side of the equation.

Next, multiply both sides of the equation by x to elminate the term with an x in the denominator.

Then, multiply both sides of the equation by 2.

In order to solve this polynomial equation, we can use the Rational Root Theorem. According to this theorem, if there is a rational root to a polynomial equation, then that root must be in the form p/q, where p is a factor of the constant, and q is the factor of the coefficient of the highest term. 

In the context of this problem, p will be a factor of 4 (which is the constant), and q will be a factor of 2 (which is the coefficient of the highest term). 

The factors of 4 are . The factors of 2 are .

This means that if there is a rational root for the equation, then the numerator must be either , and the denominator must be one of   . In other words, the possible rational roots are , because these are all the possible ratios we can make with a numerator of  and a denominator of one of .

At this point, we have narrowed down the rational roots of the equation  to the following eight choices: .

Notice, that if we were to let , then the polynomial  would evaluate to 4. Also, if we were to let , then the polynomial would evaluate to -3. Because the value of the polynomial switches from a postive value of 4 when x = 0 to a negative value of -3 when x = -1, there must be a root somewhere between  and . 

Let's see what happens when , because -1/2 is between 0 and -1. 

We will put -1/2 into the polynomial to see if it evaluates to zero.

Thus  is indeed a root to the equation. 

However, the question asks us to find the largest real root; this means that there could be other roots larger than . We will need to continue solving the equation to see what other roots are possible. 

We can make use of the Factor Theorem of polynomials, which states that if  is a root of a polynomial equation, where a is constant, then x-a must be a factor of the polynomial. 

This means that for our polynomial,  is a factor. We can divide the polynomial  by  using long division.

This means that 

In order to find the remaining roots of the equation, we now need to solve the quadratic equation .

First, divide both sides of the equation by two. 

Perhaps the most straightforward way to solve this is to use the quadratic formula:

When we evaluate this, we will be forced to take the square root of . Because this will result in an imaginary number,  has no real solutions. 

Thus, returning to our original polynomial equation , it turns out that -1/2 is indeed the only root of the equation. 

The question asks us to find the largest real value of x that solves the equation. Because -1/2 is the only real value that solves the equation, the answer must be -1/2.

The domain of a function is the set of possible values for the variable. The range would be the possible values for the solution, .

The value inside of a square root must be greater than or equal to zero in order to have a real solution.

Now we can solve for in the inequality.

Square roots have positive and negative roots, so we need to set up two results. Remember to switch the direction fo the inequality for the negative solution.

These solutions can be combined to give our final answer.

Any values of that are not included will result in an imaginary (impossible) answer.

The domain of a function includes all of the values of x for which f(x) is real and defined. In other words, if we put a value of x into the function, and we get a result that isn't real or is undefined, then that value won't be in the domain.

If we let x = 0, then we will be forced to evaluate , which is equal to 1/0. The value of 1/0 is not defined, because we can never have zero in a denominator. Thus , because f(0) isn't defined, 0 cannot be in the domain of f(x).

The answer is 0.

The domain of a function consists of all of the possible values for x. In this case, we want to make sure that we are not dividing by  ( in the denominator), since that would make our function undefined. Having  would make the denominator . Thus, that is not in our domain. There is nothing else that would make this function undefined, and thus the domain is all real numbers except

The range of a function is all of the possible values that the equation can take. For this equation our value cannot be negative, as a negative number squared still gives us a positive value.

Since , we know that the lowest possible value that can reach is . Therefore the range is .

Domain represents all possible values for . In this situation, we want to make sure that the numbers under the square root are greater than or equal to 0. This will be the case when . Thus, the domain includes all real numbers such that . 

The range of a function is defined as the possible values for , or the possible outcomes. In this function, it is not possible to get any sort of negative number as an outcome. It is possible to get zero when . Thus, the range is all real numbers greater than or equal to 0. 

The domain includes the values that go into a function (the x-values) and the range are the values that come out (the  or y-values). A sine curve represent a wave the repeats at a regular frequency. Based upon this graph, the maximum  is equal to 1, while the minimum is equal to –1. The x-values span all real numbers, as there is no limit to the input fo a sine function. The domain of the function is all real numbers and the range is .

Using  as the input () value for this equation generates an output () value that contradicts the stated condition of .

Therefore  is not a valid value for  and not in the equation's domain: