All High School Math Resources
Example Questions
Example Question #1 : Circle Functions
Find the 
To find the 


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:

We can then solve these two equations to obtain 
Example Question #2 : Circle Functions
Find the 
To find the 


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:

We can then solve these two equations to obtain
Example Question #31 : Functions And Graphs
Find the center and radius of the circle defined by the equation:
The equation of a circle is: 


In this problem, the equation is already in the format required to determine center and radius. To find the 



Example Question #1 : Circle Functions
Find the center and radius of the circle defined by the equation:
The equation of a circle is: 


In this problem, the equation is already in the format required to determine center and radius. To find the 





Example Question #1 : Polynomial Functions
It took Jack 25 minutes to travel 14 miles, what was Jack's average speed in mph?
* We have to change the time from minutes to hours, there are 60 minutes in one hour.
Example Question #2 : Polynomial Functions
Let 


Substitute 




Example Question #3 : Understanding Polynomial Functions
Solve the following system of equations:
Infinite solutions.
We will solve this system of equations by Elimination. Multiply both sides of the first equation by 2, to get:
Then add this new equation, to the second original equation, to get:
or
Plugging this value of 
or
Example Question #1683 : High School Math
List the transformations that have been enacted upon the following equation:
vertical stretch by a factor of 1/4
horizontal compression by a factor of 1/6
vertical translation 7 units down
horizontal translation 3 units right
vertical compression by a factor of 4
horizontal stretch by a factor of 6
vertical translation 7 units down
horizontal translation 3 units right
vertical stretch by a factor of 4
horizontal compression by a factor of 6
vertical translation 7 units down
horizontal translation 3 units right
vertical stretch by a factor of 4
horizontal stretch by a factor of 6
vertical translation 7 units down
horizontal translation 3 units right
vertical stretch by a factor of 4
horizontal compression by a factor of 6
vertical translation 7 units down
horizontal translation 3 units left
vertical stretch by a factor of 4
horizontal compression by a factor of 6
vertical translation 7 units down
horizontal translation 3 units right
Since the equation given in the question is based off of the parent function 

- If
is greater than 1, the function has been vertically stretched (expanded) by a factor of
.
- If
is between 0 and 1, the function has been vertically compressed by a factor of
.
In this case, 

- If
is greater than 1, the function has been horizontally compressed by a factor of
.
- If
is between 0 and 1, the function has been horizontally stretched (expanded) by a factor of
.
In this case, 

- If
is positive, the function was translated
units right.
- If
is negative, the function was translated
units left.
In this case, 

- If
is positive, the function was translated
units up.
- If
is negative, the function was translated
units down.
In this case, 
Example Question #1 : Distributions And Curves
Which of the following populations has a precisely normal distribution?
A normal distribution is one in which the values are evenly distributed both above and below the mean. A population has a precisely normal distribution if the mean, mode, and median are all equal. For the population of 3,4,5,5,5,6,7, the mean, mode, and median are all 5.
Example Question #1 : Basic Statistics
If a population has a normal distribution, the number of values within one positive standard deviation of the mean will be . . .
fewer than 20% of all values in the population
at least 40% of all values in the population
equal to the number of values within one negative standard deviation of the mean
fewer than the number of values within one negative standard deviation of the mean
equal to the number of values within two negative standard deviations of the mean
equal to the number of values within one negative standard deviation of the mean
In a normal distribution, the number of values within one positive standard deviation of the mean is equal to the number of values within one negative standard deviation of the mean. The reason for this is that the values below the population mean exactly parallel the values above the mean.
All High School Math Resources






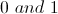











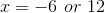







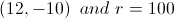





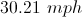

























![f(x)=4[6(x-3)]^{4}-7](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/106187/gif.latex)
![g(x) = a[b(x-c)^{4}]+d](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/106188/gif.latex)








