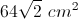We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Geometry

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #3 : How To Find The Area Of A Square

Freddie is building a square pen for his pig. He plans to buy x feet of fencing to build the pen. This will result in a pen with an area of p square feet. Unfortunately, he only has enough money to buy one third of the planned amount of fencing. Which expression represents the area of the pen he can build with this limited amount of fencing?

Possible Answers:

p/9

p/3

p/6

Correct answer:

p/9

Explanation:

If Freddie uses x feet of fencing makes a square, each side must be x/4 feet long. The area of this square is (x/4)² = x²/16 = p square feet.

If Freddie uses one third of x feet of fencing makes a square, each side must be x/12 feet long. The area of this square is (x/12)² = x²/144 = 1/9(x²/16) = 1/9(p) = p/9 square feet.

Alternate method:

The scale factor between the small perimeter and the larger perimeter = 1 : 3. Since we're comparing area, a two-dimensional measurement, we can square the scale factor and see that the ratio of the areas is 1²: 3² = 1 : 9.

Report an Error

Example Question #4 : How To Find The Area Of A Square

If the diagonal of a square measures $16\sqrt{2} \ cm$ , what is the area of the square?

Possible Answers:

$64\sqrt{2}\ cm^{2}$

$512\ cm^{2}$

$128\ cm^{2}$

$256\ cm^{2}$

$32\sqrt{2}\ cm^{2}$

Correct answer:

$256\ cm^{2}$

Explanation:

This is an isosceles right triangle, so the diagonal must equal $\sqrt{2}$ times the length of a side. Thus, one side of the square measures $16\ cm$ , and the area is equal to $(16 \ cm)^{2} = 256\ cm^{2}$

Report an Error

Example Question #12 : Quadrilaterals

A square $A$ has side lengths of $z$ . A second square $B$ has side lengths of $2.25z$ . How many $A's$ can you fit in a single $B$ ?

Possible Answers:

$4$

$1$

$5.06$

$2.25$

$3$

Correct answer:

$5.06$

Explanation:

The area of $A$ is $n$ , the area of $B$ is $5.0625n$ . Therefore, you can fit 5.06 $A's$ in $B$ .

Report an Error

Example Question #5 : How To Find The Area Of A Square

The perimeter of a square is $12\ in.$ If the square is enlarged by a factor of three, what is the new area?

Possible Answers:

$48\ in.^{2}$

$9\ in.^{2}$

$36\ in.^{2}$

$27\ in.^{2}$

$81\ in.^{2}$

Correct answer:

$81\ in.^{2}$

Explanation:

The perimeter of a square is given by $P=4s=12$ so the side length of the original square is $3\ in.$ The side of the new square is enlarged by a factor of 3 to give $s=9\ in.$

So the area of the new square is given by $A = s^{2} = (9)^{2} = 81 in^{2}$ .

Report an Error

Example Question #4 : How To Find The Area Of A Square

How much more area does a square with a side of 2r have than a circle with a radius r? Approximate π by using 22/7.

Possible Answers:

1/7 square units

4/7 square units

6/7 square units

12/14 square units

Correct answer:

6/7 square units

Explanation:

The area of a circle is given by A = πr² or 22/7r²

The area of a square is given by A = s² or (2r)² = 4r²

Then subtract the area of the circle from the area of the square and get 6/7 square units.

Report an Error

Example Question #33 : Squares

If the perimeter of a square is 44 centimeters, what is the area of the square in square centimeters?

Possible Answers:

$\dpi{100} \small 144$

$\dpi{100} \small 88$

$\dpi{100} \small 81$

$\dpi{100} \small 121$

$\dpi{100} \small 100$

Correct answer:

$\dpi{100} \small 121$

Explanation:

Since the square's perimeter is 44, then each side is $\dpi{100} \small \frac{44}{4}=11$ .

Then in order to find the area, use the definition that the

$\dpi{100} \small Area=side^{2}$

$\dpi{100} \small 11^{2}=121$

Report an Error

Example Question #6 : How To Find The Area Of A Square

Midpointsquare

Given square ABCD , with midpoints on each side connected to form a new, smaller square. How many times bigger is the area of the larger square than the smaller square?

Possible Answers:

$2\sqrt{2}$

$\frac{\sqrt{2}}{2}$

$\sqrt{2}$

Correct answer:

Explanation:

Assume that the length of each midpoint is 1. This means that the length of each side of the large square is 2, so the area of the larger square is 4 square units. $A=s^{2}$

To find the area of the smaller square, first find the length of each side. Because the length of each midpoint is 1, each side of the smaller square is $\sqrt{2}$ (use either the Pythagorean Theorem or notice that these right trianges are isoceles right trianges, so $s, s, s\sqrt{2}$ can be used).

The area then of the smaller square is 2 square units.

Comparing the area of the two squares, the larger square is 2 times larger than the smaller square.

Report an Error

Example Question #11 : How To Find The Area Of A Square

Square_with_diagonal

Find the area of a square with a diagonal of d=2.5cm .

Possible Answers:

Not enough information to solve

$5.0cm^{2}$

$\dpi{100} 4.25cm^{2}$

$6.25cm^{2}$

$3.125cm^{2}$

Correct answer:

$3.125cm^{2}$

Explanation:

A few facts need to be known to solve this problem. Observe that the diagonal of the square cuts it into two right isosceles triangles; therefore, the length of a side of the square to its diagonal is the same as an isosceles right triangle's leg to its hypotenuse: $1:\sqrt{2}$ .

$\frac{s}{d}=\frac{1}{\sqrt{2}}$

$\dpi{100} \frac{s}{2.5cm}=\frac{1}{\sqrt{2}}$

Rearrange an solve for .

$s=\frac{2.5cm}{\sqrt{2}}$

Now, solve for the area using the formula $A=s^{2}$ .

$A=(\frac{2.5cm}{\sqrt{2}})^{2}$

$\dpi{100} A=\frac{6.25cm^{2}}{2}$

$\rightarrow 3.125cm^{2}$

Report an Error

Example Question #241 : Geometry

If the ratio of the sides of two squares is 2:1 , what is the ratio of the areas of those two squares?

Possible Answers:

8:1

6:1

4:1

2:1

Correct answer:

4:1

Explanation:

Express the ratio of the two sides of the squares as x:y = 2:1 . The area of each square is one side multiplied by itself, so the ratios of the areas would be x^2:y^2 = 2^2:1^2 . The right side of this equation simplifies to a ratio of 4:1 .

Report an Error

Example Question #11 : How To Find The Area Of A Square

If a completely fenced-in square-shaped yard requires 140 feet of fence, what is the area, in square feet, of the lot?

Possible Answers:

140

1225

4900

Correct answer:

1225

Explanation:

Since the yard is square in shape, we can divide the perimeter(140ft) by 4, giving us 35ft for each side. We then square 35 to give us the area, 1225 feet.

Report an Error

View Tutors

Abhisek
Certified Tutor

University of Florida, Bachelor of Engineering, Computer Science.

View Tutors

Mandy
Certified Tutor

The University of Texas at El Paso, Bachelor in Arts, Education. Capella University, Masters in Education, Education.

View Tutors

Aaron
Certified Tutor

University of Dallas, Bachelor of Science, Chemistry. Texas A & M University-College Station, Doctor of Philosophy, Nuclear E...

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Los Angeles, LSAT Tutors in Washington DC, Reading Tutors in San Diego, GRE Tutors in Houston, ACT Tutors in Boston, Computer Science Tutors in Phoenix, SAT Tutors in Boston, Computer Science Tutors in San Francisco-Bay Area, LSAT Tutors in Seattle, Calculus Tutors in Phoenix

Popular Courses & Classes

Spanish Courses & Classes in Washington DC, MCAT Courses & Classes in Philadelphia, GRE Courses & Classes in Denver, LSAT Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in New York City, GMAT Courses & Classes in Philadelphia, GMAT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Chicago, LSAT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Houston

Popular Test Prep

ISEE Test Prep in Miami, GRE Test Prep in Denver, ISEE Test Prep in Chicago, SAT Test Prep in Boston, MCAT Test Prep in San Francisco-Bay Area, ISEE Test Prep in Houston, GRE Test Prep in Boston, MCAT Test Prep in Chicago, MCAT Test Prep in Philadelphia, ACT Test Prep in Los Angeles

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Geometry

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #3 : How To Find The Area Of A Square

Example Question #4 : How To Find The Area Of A Square

Example Question #12 : Quadrilaterals

Example Question #5 : How To Find The Area Of A Square

Example Question #4 : How To Find The Area Of A Square

Example Question #33 : Squares

Example Question #6 : How To Find The Area Of A Square

Example Question #11 : How To Find The Area Of A Square

Example Question #241 : Geometry

Example Question #11 : How To Find The Area Of A Square

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: