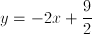First we must find the slope of the given line. The slope of y = –3x – 4 is –3. The slope of the perpendicular line is the negative reciprocal. This means you change the sign of the slope to its opposite: in this case to 3. Then find the reciprocal by switching the denominator and numerator to get 1/3; therefore the slope of the perpendicular line is 1/3.

The question puts the line in point-slope form y – y₁ = m(x – x₁), where m is the slope. Therefore, the slope of the original line is 1/2.  A line perpendicular to another has a slope that is the negative reciprocal of the slope of the other line. The negative reciprocal of the original line is –2, and is thus the slope of its perpendicular line. 

The equation of a line is  where  is the slope.

Rearrange the equation to match this:

For the perpendicular line, the slope is the negative reciprocal;

therefore 

The slope of a perpendicular line is the opposite reciporical of the originial slope.  

The opposite would be changing the sign from positive to negative or vice versa.  

The reciporical is flipping the fraction or switching the numerator and denominator.  

This equation is in slope-intercept form,

meaning m represents the slope of the equation.

Since the original is  , then the perpendicular would be positive and would swtich the 7 and 3 giving us .

Perpendicular lines have opposite and reciprocal slopes.  Therefore, let us find the slope of our line and appropriately modify it to find the perpendicular line.  To find the slope of our line, remember that in the slope-intercept form (y = mx + b), m represents the slope.

3x + 4y = 5  => 4y = 5 - 3x  => y = (-3/4)x + 5/4

Therefore, the slope of our line is -3/4.  The perpendicular to this would be 4 / 3.  Therefore, only y = (4/3)x - 15 is perpendicular.

To solve this, we need to use the point-slope form.  However, to do this, we need to ascertain the slope of the perpendicular line.  For this, get 8y + 4x = 10 into slope-intercept form:

8y = -4x + 10; y = (-1/2)x + 1.25

Therefore, the slope of this line is -1/2 and its perpendicular (opposite and reciprocal) slope is 2.

The point slope form is: (y – y1) = m * (x – x1)

For our data it is: y – 4 = 2 * (x – 5)

Simplifying, we get: y – 4 = 2 x – 10; y = 2x – 6

Rewrite the equation in form.

The perpendicular line will have a slope which is the negative reciprocal of the slope .

To find if something is perpendicular, you need to first know the slope of your given line.  Based on your points, this is easy.  Recall that slope is merely:

This is:

Since a perpendicular line has a slope that is both opposite in sign and reciprocal, you need to choose a line with a slope of .  The only possible option is, therefore, 

To find if something is perpendicular, you need to first know the slope of your given line. Based on your points, this is easy. Recall that slope is merely:

This is:

Since a perpendicular line has a slope that is both opposite in sign and reciprocal, you need to choose a line with a slope of .  The only possible option is, therefore, 

easiest way to do this is by plotting the points and turining it into a right triangle by using delta x and delta y

the delta x is 11-6 = 5

the delta y is 15-3 = 12

those form the two legs of the right triangle; the hypotenuse is the distance

dx² +dy²= h²

25+144 = h²

169 = h²

h = 13