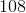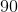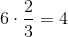GRE Math : Geometry

Study concepts, example questions & explanations for GRE Math

Create An Account

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Surface Area Of A Cylinder

What is the surface area of a cylinder that has a diameter of 6 inches and is 4 inches tall?

Possible Answers:

$12\pi$

$15\pi$

$4\pi$

$10\pi$

$42\pi$

Correct answer:

$42\pi$

Explanation:

The formula for the surface area of a cylinder is $\dpi{100} 2\pi r^{2}+ 2\pi rh$ ,

where is the radius and is the height.

$\dpi{100} SA=2\pi (3)^{2}+2\pi (3)(4)$

$\dpi{100} =42\pi$

Report an Error

Example Question #1 : Cylinders

A cylinder has a radius of 4 and a height of 8. What is its surface area?

Possible Answers:

$32\pi$

$100\pi$

$96\pi$

$64\pi$

$128\pi$

Correct answer:

$96\pi$

Explanation:

This problem is simple if we remember the surface area formula!

$SA = 2\pi r^2 +2\pi rh = 2\pi *16+2\pi *4*8 = 32\pi +64\pi = 96\pi$

Report an Error

Example Question #3 : How To Find The Surface Area Of A Cylinder

Quantitative Comparison

Quantity A: Surface area of a cylinder that is 2 feet high and has a radius of 4 feet

Quantity B: Surface area of a box that is 3 feet wide, 2 feet high, and 4 feet long

Possible Answers:

Quantity A is greater.

The two quantities are equal.

The relationship cannot be determined from the information given.

Quantity B is greater.

Correct answer:

Quantity A is greater.

Explanation:

Quantity A: SA of a cylinder = 2πr² + 2πrh = 2π * 16 + 2π * 4 * 2 = 48π

Quantity B: SA of a rectangular solid = 2ab + 2bc + 2ac = 2 * 3 * 2 + 2 * 2 * 4 + 2 * 3 * 4 = 52

48π is much larger than 52, because π is approximately 3.14.

Report an Error

Example Question #1 : Cylinders

A cylinder has a height of 4 and a circumference of 16π. What is its volume

Possible Answers:

256π

16π

none of these

128π

64π

Correct answer:

256π

Explanation:

circumference = πd

d = 2r

volume of cylinder = πr²h

r = 8, h = 4

volume = 256π

Report an Error

Example Question #1 : How To Find The Volume Of A Cylinder

Rusty is considering making a cylindrical grain silo to store his crops. He has an area that is 6 feet long, 6 feet wide and 12 feet tall to build a cylinder in. What is the maximum volume of grain that he can store in this cylinder?

Possible Answers:

$54\pi$

432

108

$108\pi$

$432\pi$

Correct answer:

$108\pi$

Explanation:

The maximum cylindrical base can have a diameter of 6 and therefore a radius of 3. The formula for the volume of a cylinder is 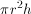$\dpi{100} \small \pi r^{2}h$ , which in this case is $\dpi{100} \small 3\times 3\times 12\times \pi$ .

Report an Error

Example Question #2 : How To Find The Volume Of A Cylinder

A cylinder with volume of $192\pi\:in^3$ and a radius of $4\:in$ has its radius doubled. What is the volume of the new cylinder?

Possible Answers:

$384\pi\:in^3$

$528\pi\:in^3$

$768\pi\:in^3$

$1536\pi\:in^3$

$892\pi\:in^3$

Correct answer:

$768\pi\:in^3$

Explanation:

To begin, you must solve for the height of the original cylinder. We know:

$V=\pi r^2h$

For our values, we know:

$192\pi=\pi 4^2h=16\pi h$

Now, divide both sides by $16\pi$ :

12=h

So, if we have a new radius of , our volume will be:

$V=8^2*12*\pi=768\pi\:in^3$

Report an Error

Example Question #11 : Solid Geometry

If the dimensions of a rectangular crate are $6\times 7\times 8$ , which of the following CANNOT be the total surface area of two sides of the crate?

Possible Answers:

112

104

Correct answer:

Explanation:

Side 1: surface area of the 6 x 7 side is 42

Side 2: surface area of the 7 x 8 side is 56

Side 3: surface area of the 6 x 8 side is 48.

We can add sides 1 and 3 to get 90, so that's not the answer.

We can add sides 1 and 1 to get 84, so that's not the answer.

We can add sides 2 and 3 to get 104, so that's not the answer.

We can add sides 2 and 2 to get 112, so that's not the answer.

This leaves the answer of 92. Any combination of the three sides of the rectangular prism will not give us 92 as the total surface area.

Report an Error

Example Question #314 : Geometry

Kate wants to paint a cylinder prism.

What is the surface area of her prism if it is inches tall and has a diameter of inches? Round to the nearest whole number.

Possible Answers:

70in^2

70.7in^2

43in^2

71in^2

Correct answer:

71in^2

Explanation:

First, find the area of the base of the cyclinder:

$\pi r^2=\pi(1.5)^2=2.25\pi$ and multiply that by two, since there are two sides with this measurement: $2.25\pi\cdot2=4.5\pi$ .

Then, you find the width of the rectangular portion (label portion) of the prism by finding the circumference of the cylinder:

$\pi\cdot d=\pi\cdot3=3\pi$ . This is then multiplied by the height of the cylinder to find the area of the rectanuglar portion of the cylinder: $3\pi\cdot6=18\pi$ .

Finally, add all sides together and round: $4.5\pi+18\pi=70.7=71in^2$ .

Report an Error

Example Question #2 : How To Find The Surface Area Of A Prism

Prism_1_454590 This triangular prism has a height of feet and a length of feet.

What is the surface area of the prism? Round to the nearest tenth.

Possible Answers:

90ft^2

80ft^2

81ft^2

80.7 ft^2

Correct answer:

80.7 ft^2

Explanation:

Find the area of the triangular sides first:

$\frac{b\cdot h}{2}=\frac{3\cdot3}{2}=\frac{9}{2}=4.5.$

Since there are two sides of this area, we multiply the area by 2:

$4.5\cdot 2=9.$

Next find the area of the rectangular regions. Two of them have the width of 3 feet and a length of 7 feet, while the last one has a width measurement of $3\sqrt{2}$ feet and a length of 7 feet. Multiply and add all other sides:

$(3\cdot7)+(3\cdot7)+(3\sqrt2\cdot7)=21+21+21\sqrt2$ .

Lastly, add the triangular sides to the rectangular sides and round:

$9+21+21+21\sqrt2=80.7ft^2$ .

Report an Error

Example Question #1 : How To Find The Volume Of A Prism

A rectangular prism has a width of 3 units, a length that is twice the width, and a height that is two-thirds the length. What is the volume of the prism?

Possible Answers:

units^3

Correct answer:

units^3

Explanation:

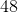
Remember, the formula for the volume of a rectangular prism is width times height times length:

$V=w\cdot h\cdot l$

Now, let's solve the word problem for each of these values. We know that W=3 . If length is double the width, then the length must be 6 units. If the height is two-thirds the length, then the height must be 4:

$6\cdot \frac{2}{3}=4$

Multiply all three values together to solve for the volume:

$V=w\cdot h\cdot l$

$V=3\cdot 4\cdot 6$

V = 72 units^3

The volume of the rectangular prism is units cubed.

Report an Error

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Computer Science Tutors in Boston, Calculus Tutors in Dallas Fort Worth, Calculus Tutors in Washington DC, Chemistry Tutors in Phoenix, MCAT Tutors in Los Angeles, Spanish Tutors in Denver, Math Tutors in Seattle, ISEE Tutors in Seattle, Computer Science Tutors in Denver, GMAT Tutors in Philadelphia

Popular Courses & Classes

SSAT Courses & Classes in San Diego, ISEE Courses & Classes in Atlanta, SAT Courses & Classes in Atlanta, GMAT Courses & Classes in Houston, SAT Courses & Classes in Washington DC, GMAT Courses & Classes in Seattle, SSAT Courses & Classes in Philadelphia, MCAT Courses & Classes in Philadelphia, Spanish Courses & Classes in Washington DC, ISEE Courses & Classes in Denver

Popular Test Prep

GMAT Test Prep in Phoenix, GMAT Test Prep in Chicago, SSAT Test Prep in Miami, GRE Test Prep in Denver, GRE Test Prep in Dallas Fort Worth, ACT Test Prep in Chicago, GRE Test Prep in Phoenix, SSAT Test Prep in New York City, LSAT Test Prep in Dallas Fort Worth, LSAT Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

Email address:
Your name:
Feedback:

GRE Math : Geometry

Study concepts, example questions & explanations for GRE Math

All GRE Math Resources

Example Questions

Example Question #1 : How To Find The Surface Area Of A Cylinder

Example Question #1 : Cylinders

Example Question #3 : How To Find The Surface Area Of A Cylinder

Example Question #1 : Cylinders

Example Question #1 : How To Find The Volume Of A Cylinder

Example Question #2 : How To Find The Volume Of A Cylinder

Example Question #11 : Solid Geometry

Example Question #314 : Geometry

Example Question #2 : How To Find The Surface Area Of A Prism

Example Question #1 : How To Find The Volume Of A Prism

All GRE Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details