We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Differential Equations : Differential Equations

Study concepts, example questions & explanations for Differential Equations

Create An Account

All Differential Equations Resources

1 Diagnostic Test 29 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : Matrix Exponentials

Use the definition of matrix exponential,

$e^{At}=I+At+A^2\frac{t^2}{2!}+...+A^k\frac{t^k}{k!}+...=\sum_{k=0}^\infty A^k\frac{t^k}{k!}$

to compute $e^{At}$ of the following matrix.

$A=\begin{pmatrix} 0& 1\\ 2&1 \end{pmatrix}$

Possible Answers:

$e^{At}=\begin{pmatrix} 0&1\\ e^{2t}&e^t \end{pmatrix}$

$e^{At}=\begin{pmatrix} 0&e^t \\ 2e^{t}&e^t \end{pmatrix}$

$e^{At}=\begin{pmatrix} 0&e^t \\ e^{2t}&e^t \end{pmatrix}$

$e^{At}=\begin{pmatrix} 0&e^t \\ e^{2t}&1\end{pmatrix}$

$e^{At}=\begin{pmatrix} 0&e^t \\ e^{2t}&2e^t \end{pmatrix}$

Correct answer:

$e^{At}=\begin{pmatrix} 0&e^t \\ e^{2t}&e^t \end{pmatrix}$

Explanation:

Given the matrix,

$A=\begin{pmatrix} 0& 1\\ 2&1 \end{pmatrix}$

and using the definition of matrix exponential,

$e^{At}=I+At+A^2\frac{t^2}{2!}+...+A^k\frac{t^k}{k!}+...=\sum_{k=0}^\infty A^k\frac{t^k}{k!}$

calculate

$A^2=AA=\begin{pmatrix} 0&1 \\ 2&1 \end{pmatrix} \begin{pmatrix} 0&1 \\ 2&1 \end{pmatrix}=\begin{pmatrix} 0& 1\\ 4& 1 \end{pmatrix}$

$A^3=A^2A=\begin{pmatrix} 0&1 \\ 4&1 \end{pmatrix} \begin{pmatrix} 0&1 \\ 2&1 \end{pmatrix}=\begin{pmatrix} 0&1 \\ 8&1 \end{pmatrix}$

Therefore

$A^k=\begin{pmatrix} 0&1 \\ 2^k&1 \end{pmatrix}; k=1,2,3,...$

$e^{At}=I+\frac{A}{1!}t+\frac{A^2}{2!}t^2+...$

$\begin{pmatrix} 0& 1\\ 2&1 \end{pmatrix}+\frac{1}{1!}\begin{pmatrix} 0& 1\\ 4&1 \end{pmatrix}+\frac{1}{3!}\begin{pmatrix} 0& 1\\ 8&1 \end{pmatrix}$

$e^{At}=\begin{pmatrix} 0&e^t \\ e^{2t}&e^t \end{pmatrix}$

Report an Error

Example Question #13 : System Of Linear First Order Differential Equations

Calculate the matrix exponential, $e^{tA}$ , for the following matrix: $A = \begin{bmatrix} -7& 3\\-1 &-3 \end{bmatrix}$ .

Possible Answers:

$\frac{1}{2}\begin{bmatrix} 3e^{-6t}-e^{-4t} & -3e^{-6t} + 3 e^{-4t} \\ e^{-6t}-e^{-4t}&-e^{-6t} + 3e^{-4t} \end{bmatrix}$

$\frac{1}{2}\begin{bmatrix} 3e^{-5t}-e^{-3t} & -3e^{-5t} + 3 e^{-3t} \\ e^{-5t}-e^{-3t}&-e^{-5t} + 3e^{-3t} \end{bmatrix}$

$\begin{bmatrix} 10e^{-5t}-2e^{-3t} & -e^{-5t} + 3 e^{-3t} \\ 2e^{-5t}-e^{-3t}&e^{-5t} + 4e^{-3t} \end{bmatrix}$

$\begin{bmatrix} 3e^{-5t}-e^{-3t} & -3e^{-5t} + 3 e^{-3t} \\ e^{-5t}-e^{-3t}&-e^{-5t} + 3e^{-3t} \end{bmatrix}$

$\begin{bmatrix} e^{-6t}-3e^{-4t} & -5e^{-6t} + e^{-4t} \\ e^{-6t}-e^{-4t}&-e^{-6t} + 8e^{-4t} \end{bmatrix}$

Correct answer:

$\frac{1}{2}\begin{bmatrix} 3e^{-6t}-e^{-4t} & -3e^{-6t} + 3 e^{-4t} \\ e^{-6t}-e^{-4t}&-e^{-6t} + 3e^{-4t} \end{bmatrix}$

Explanation:

To get the matrix exponential, we will have to diagonalize the matrix, which requires us to find the eigenvalues and eigenvectors. Thus, we have

$\begin{vmatrix} \lambda+7 &-3 \\ 1& \lambda +3 \end{vmatrix} = (\lambda+7)(\lambda+3) +3 = \lambda^2 + 10\lambda +24 = (\lambda + 6)(\lambda + 4) = 0$

Using $\lambda = -4, -6$ , we then find the eigenvectors by solving for the eigenspace.

$\lambda = -4$

$\begin{bmatrix} 3 & -3 &\vline &0 \\ 1& -1 &\vline & 0 \end{bmatrix} \rightarrow \begin{bmatrix} 1 & -1 &\vline &0 \\ 0& 0 &\vline & 0 \end{bmatrix}$

This has solutions x_1 - x_2 = 0 , or $x_1\begin{bmatrix} 1\\ 1 \end{bmatrix}$ . So a suitable eigenvector is simply $\begin{bmatrix} 1\\1 \end{bmatrix}$ .

Repeating for $\lambda = -6$ ,

$\begin{bmatrix} 1 & -3 &\vline &0 \\ 1& -3 &\vline & 0 \end{bmatrix} \rightarrow \begin{bmatrix} 1 & -3 &\vline &0 \\ 0& 0 &\vline & 0 \end{bmatrix}$

This has solutions x_1 - 3x_2 = 0 , and thus a suitable eigenvector is $\begin{bmatrix} 3\\1 \end{bmatrix}$ .

Thus, we have $P = \begin{bmatrix} 1 & 3\\ 1 & 1 \end{bmatrix}$ , $D = \begin{bmatrix} -4 &0 \\ 0& -6 \end{bmatrix}$ , and using the inverse formula for 2x2 matrices, $P^{-1} = -\frac{1}{2}\begin{bmatrix} 1 &-3 \\ -1 &1 \end{bmatrix}$ . Now we just take the matrix exponential of and multiply the three matrices back together. Thus,

$e^{tA} = Pe^{tD}P^{-1} = -\frac{1}{2}\begin{bmatrix} 1 &3 \\ 1& 1 \end{bmatrix}\begin{bmatrix} e^{-4t} &0 \\ 0& e^{-6t} \end{bmatrix}\begin{bmatrix} 1 &-3 \\ -1&1 \end{bmatrix}$

Multiplying these out yields $e^{tA} = \frac{1}{2}\begin{bmatrix} 3e^{-6t}-e^{-4t} & -3e^{-6t} + 3 e^{-4t} \\ e^{-6t}-e^{-4t}&-e^{-6t} + 3e^{-4t} \end{bmatrix}$

Report an Error

Example Question #1 : Matrix Exponentials

Find the general solution to

$y^{'''} + y^{''} + 3y' - 5y = 0$

Possible Answers:

$y(x) = C_1e^x + C_2e^{-x}\cos{2x} + C_3e^{-x}\sin{2x}$

$y(x) = C_1e^x + C_2e^{-x}\cos{x} + C_3e^{-x}\sin{x}$

$y(x) = C_1e^x + C_2e^{-x}\cos{2x}$

None of the other answers

$y(x) = C_1e^x + C_2e^{-x}\sin{2x}$

Correct answer:

$y(x) = C_1e^x + C_2e^{-x}\cos{2x} + C_3e^{-x}\sin{2x}$

Explanation:

The auxiliary equation is

r^3+r^2+3r-5 = (r-1)(r^2+2r+5) = 0

The roots are

$r = 1, -1 \pm 2i$

Our solution is

$y(x) = C_1e^x + C_2e^{-x}\cos{2x} + C_3e^{-x}\sin{2x}$

Report an Error

Example Question #1 : The Laplace Transform

Find the Laplace Transform for the following function.

$\mathcal{L}\begin{Bmatrix} e^{-5t} \end{Bmatrix}$

Possible Answers:

$\mathcal{L}\begin{Bmatrix} e^{-5t} \end{Bmatrix}=\frac{1}{s-5}, s>-5$

$\mathcal{L}\begin{Bmatrix} e^{-5t} \end{Bmatrix}=\frac{1}{s+3}, s>-5$

$\mathcal{L}\begin{Bmatrix} e^{-5t} \end{Bmatrix}=\frac{1}{s+5}, s>5$

$\mathcal{L}\begin{Bmatrix} e^{-5t} \end{Bmatrix}=\frac{1}{s+5}, s<-5$

$\mathcal{L}\begin{Bmatrix} e^{-5t} \end{Bmatrix}=\frac{1}{s+5}, s>-5$

Correct answer:

$\mathcal{L}\begin{Bmatrix} e^{-5t} \end{Bmatrix}=\frac{1}{s+5}, s>-5$

Explanation:

To find the Laplace Transform for the following function

$\mathcal{L}\begin{Bmatrix} e^{-5t}\end{Bmatrix}$

use the transforms for basic functions which state,

$\mathcal{L}\begin{Bmatrix} 1 \end{Bmatrix}=\frac{1}{s}$

$\mathcal{L}\begin{Bmatrix} e^{at} \end{Bmatrix}=\frac{1}{s-a}$

$\mathcal{L}\begin{Bmatrix} e^{-5t} \end{Bmatrix}=\int_0^\infty e^{-st}e^{-5t}dt=\int_0^\infty e^{-(s+5)t} dt$

$\\=\frac{-e^{-(s+5)t}}{s+5}\bigg|_0^\infty \\\\=\frac{1}{s+5}, s>-5$

Report an Error

Example Question #2 : The Laplace Transform

Find the Laplace transform of the periodic function.

$S(t)=\left\{\begin{matrix} 1,& 0\leq2\\ 0, & 2\leq4 \end{matrix}\right.$

Possible Answers:

$\frac{1}{s(1+e^{-2s})(1+e^{s})}$

$\frac{1}{s(1-e^{-2s})(1+e^{-s})}$

$\frac{1}{s(1+e^{-2s})(1+e^{-s})}$

$\frac{1}{s(1+e^{2s})(1+e^{-s})}$

$\frac{1}{s(1+e^{-2s})(1-e^{-s})}$

Correct answer:

$\frac{1}{s(1+e^{-2s})(1+e^{-s})}$

Explanation:

This particular piecewise function is called a square wave. The period of this function is the length at which it takes the function to return to its starting point.

For this particular function

$S(t)=\left\{\begin{matrix} 1,& 0\leq2\\ 0, & 2\leq4 \end{matrix}\right.$

it has a period of

T=4 .

and furthermore,

f(t+4)=f(t)

Using the Transform of a Periodic Function Theorem which states,

$\mathcal{L}\begin{Bmatrix} f(t) \end{Bmatrix}=\frac{1}{1-e^{-sT}}\int_0^T e^{-sT}f(t)dt$

the problem can be solved as follows.

$\mathcal{L}\begin{Bmatrix} S(t) \end{Bmatrix}=\frac{1}{1-e^{-4s}}\int_0^4 e^{-st}S(t)dt$

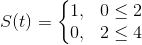
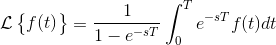
$\\=\frac{1}{1-e^{-4s}}\left[ \int_0^2 e^{-st}\cdot 1 dt+\int_2^4 e^{-st}\cdot 0dt \right] \\\\=\frac{1}{1-e^{-4s}}\frac{1-e^{-s}}{s}\\\\\leftarrow 1-e^{-4s}=(1+e^{-2s})(1-e^{-2s})\\\\\leftarrow (1-e^{-2s})=(1+e^{-s})(1-e^{-s}) \\\\=\frac{1-e^{-s}}{s(1+e^{-2s})(1-e^{-s})(1+e^{-s})} \\\\=\frac{1}{s(1+e^{-2s})(1+e^{-s})}$

Report an Error

View Differential Equations Tutors

Dereika
Certified Tutor

Southern University and A & M College, Bachelor of Science, Accounting. Grand Canyon University, Master of Science, Accounting.

View Differential Equations Tutors

Reza
Certified Tutor

University of Sherbrooke, Doctor of Philosophy, Mathematics. University of Manitoba, Master of Science, Mathematics.

View Differential Equations Tutors

Robert
Certified Tutor

Rensselaer Polytechnic Institute, Bachelors, Electrical Engineering. Brooklyn Polytechnic, Masters, Computer Science.

All Differential Equations Resources

1 Diagnostic Test 29 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SSAT Tutors in Philadelphia, GRE Tutors in San Diego, LSAT Tutors in Miami, SAT Tutors in Los Angeles, English Tutors in Washington DC, Spanish Tutors in Houston, LSAT Tutors in San Diego, ACT Tutors in Dallas Fort Worth, MCAT Tutors in Los Angeles, Algebra Tutors in Dallas Fort Worth

Popular Courses & Classes

SAT Courses & Classes in Chicago, SAT Courses & Classes in Houston, LSAT Courses & Classes in Chicago, Spanish Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Miami, LSAT Courses & Classes in Miami, LSAT Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Miami, ACT Courses & Classes in Denver

Popular Test Prep

SSAT Test Prep in Miami, GRE Test Prep in Boston, LSAT Test Prep in Denver, ISEE Test Prep in San Diego, SSAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in San Diego, SSAT Test Prep in New York City, GMAT Test Prep in Dallas Fort Worth, SAT Test Prep in Chicago, SAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Differential Equations : Differential Equations

Study concepts, example questions & explanations for Differential Equations

All Differential Equations Resources

Example Questions

Example Question #2 : Matrix Exponentials

Example Question #13 : System Of Linear First Order Differential Equations

Example Question #1 : Matrix Exponentials

Example Question #1 : The Laplace Transform

Example Question #2 : The Laplace Transform

All Differential Equations Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: