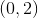This equation can be put into the form  as follows:

. Differential equations in this form can be solved by use of integrating factor. To solve, take  and solve for 

Note, when using integrating factors, the +C constant is irrelevant as we only need one solution, not infinitely many. Thus, we have set C to 0.

Next, note that 

Or more simply, . Integrating both sides using substitution of variables we find

Finally dividing by , we see

. Plugging in our initial condition,

So 

And .

The term  makes the differential equation nonlinear because a linear equation has the form of 

First, divide by  on both sides of the equation.

Identify the factor  term.

Integrate the factor.

Substitute this value back in and integrate the equation.

Now divide by  to get the general solution.

The transient term means a term that when the values get larger the term itself gets smaller. Therefore the transient term for this function is 

For a differential equation to be exact, two things must be true. First, it must take the form . In our case, this is true, with  and . The second condition is that . Taking the partial derivatives, we find that  and . As these are equal, we have an exact equation.

Next we find a  such that  and . To do this, we can integrate  with respect to  or we can integrate  with respect to  Here, we choose arbitrarily to integrate .

We aren't quite done yet, because when taking a multivariate integral, the constant of integration can now be a function of y instead of just a constant. However, we know that , so taking the partial derivative, we find that  and thus that  and .

We now know that , and the point of finding psi was so that we could rewrite , and because the derivative of psi is 0, we know it must have been a constant. Thus, our final answer is 

.

If you have an initial value, you can solve for c and have an implicit solution.

For a differential equation to be exact, two things must be true. First, it must take the form . In our case, this is true, with  and . The second condition is that . Taking the partial derivatives, we find that  and . As these are unequal, we do not have an exact equation.

Since this is in the form of a linear equation

we calculate the integration factor

Multiplying by  we get

Integrating

Plugging in the Initial Condition to solve for the Constant we get

Our solution is

This is a Bernoulli Equation of the form

which requires a substitution

to transform it into a linear equation

Rearranging our equation gives us

Substituting 

Solving the linear ODE gives us

Substituting in  and solving for 

Rearranging the following equation

This satisfies the test of exactness, so integrating we have

Putting the equation in standard form we get that

We need to find where these coefficients are simultaneously continuous. This is where

. The choice that is not a subset of these is 

This is a linear higher order differential equation. First, we need the characteristic equation, which is just obtained by turning the derivative orders into powers to get the following:

 We then solve the characteristic equation and find that (Use the quadratic formula if you'd like)  This lets us know that the basis for the fundamental set of solutions to this problem (solutions to the homogeneous problem) contains  .

As the given problem was homogeneous, the solution is just a linear combination of these functions. Thus, . Plugging in our initial condition, we find that . To plug in the second initial condition, we take the derivative and find that . Plugging in the second initial condition yields . Solving this simple system of linear equations shows us that 

Leaving us with a final answer of 

(Note, it would have been very simple to find the right answer just by taking derivatives and plugging in, but this is not overly helpful for non-multiple choice questions)