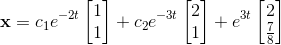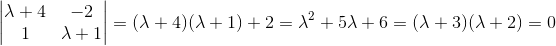So this is a homogenous, first order differential equation. In order to solve this we need to solve for the roots of the equation. This equation can be written as:

  gives us a root of  

The solution of homogenous equations is written in the form:

 so we don't know the constant, but can substitute the values we solved for the root:

We have one initial values, for y(t) with t=0

So:

This gives a final answer of:

So this is a homogenous, third order differential equation. In order to solve this we need to solve for the roots of the equation. This equation can be written as:

 Which, using the cubic formula or factoring gives us roots of ,   and 

The solution of homogenous equations is written in the form:

 so we don't know the constants, but can substitute the values we solved for the roots:

We have three initial values, one for y(t), one for y'(t), and for y''(t) all with t=0

So:

 so: 

So this can be solved either by substitution or by setting up a 3X3 matrix and reducing. Once you do either of these methods, the values for the constants will be:   Then  and 

This gives a final answer of:

So this is a homogenous, third order differential equation. In order to solve this we need to solve for the roots of the equation. This equation can be written as:

 Which, using the cubic formula or factoring gives us roots of ,   and 

The solution of homogenous equations is written in the form:

 so we don't know the constants, but can substitute the values we solved for the roots:

We have three initial values, one for y(t), one for y'(t), and for y''(t) all with t=0

So:

So this can be solved either by substitution or by setting up a 3X3 matrix and reducing. Once you do either of these methods, the values for the constants will be:   Then  and 

This gives a final answer of:

To find the general solution to the given system

first find the eigenvalues and eigenvectors.

Therefore the eigenvalues are

Now calculate the eigenvectors

For 

Thus,

For 

Thus 

Therefore,

Now the general solution is,

A saddle point phase plane results from two real eigenvalues of different signs. Three of these matrices are triangular, which means their eigenvalues are on the diagonal. For these three, the eigenvalues are real, but both the same sign, meaning they don't have saddles. For the remaining two, we'll need to find the eigenvalues using the characteristic equations.

For , we have

The discriminant to this is , so the solutions are non-real. Thus, this matrix doesn't yield a saddle point.

For  we have,

We see that this matrix yields two real eigenvalues with different signs. Thus, it is the correct choice.

Finding the eigenvalues and eigenvectors of  with the characteristic equation of the matrix

The corresponding eigenvalues are, respectively

 and 

This gives us that the general solution is

First, we will need the complementary solution, and a fundamental matrix for the homogeneous system. Thus, we find the characteristic equation of the matrix given.

Using , we then find the eigenvectors by solving for the eigenspace.

This has solutions , or . So a suitable eigenvector is simply .

Repeating for ,

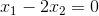
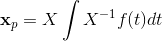
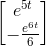
This has solutions , and thus a suitable eigenvector is . Thus, our complementary solution is  and our fundamental matrix (though in this case, not the matrix exponential) is . Variation of parameters tells us that the particular solution is given by , so first we find  using the inverse rule for 2x2 matrices. Thus, . Plugging in, we have . So  .

Finishing up, we have .

Adding the particular solution to the homogeneous, we get a final general solution of 

Given the matrix,

and using the definition of matrix exponential, 

calculate 

Therefore 

First we find our eigenvalues by finding the characteristic equation, which is the determinant of  (or ). Expansion down column one yields

Simplifying and factoring out a , we have

So our eigenvalues are 

To find the eigenvectors, we find the basis for the null space of  for each lambda.

lambda = -1

Adding row 1 to row 3 and placing into row 3, dividing row two by 6, and swapping rows two and 1 gives us our reduced row echelon form. For our purposes, it suffices just to do the first step and look at the resulting system.

So that 

Which has solutions  . Thus, a clean eigenvector here would be  

For lambda = 4, we have 

Step 1: Add row 3 to row 1.

Step 2: Add 3 row 3 to row 2

Step 3: Add -6/5 row 1 in to row 2. Swap and divide as necessary to get proper pivots.

This gives us

So that 

Which has solutions  . Thus, a clean eigenvector here would be  .

As we only ended up with two eigenvectors, we'll need to grab a generalized eigenvector as well. To do this, we will solve

(for lambda = 1, and we set it equal to the negation of our eigenvector for 1.)

This gives us

And the steps to solve this are identical to the steps to solving for the eigenvector for -1. Following them once more, and further reducing, we get.

Solving the system, our generalized eigenvector is given by . Decomposing into the Jordan matrix gives us

,

When we exponentiate this in the above form, we only need to find the matrix exponential of the Jordan matrix. This is done by exponentiating the entries on the main diagonal, and making the entries on the super diagonals of each Jordan block powers of t over the proper factorials. Thus, the matrix exponential is given by

From here, it would just be a matter of inverting and multiplying together -- daunting algebraically, but conceptually quite easy.

Note: In the final form above, anything with the same entries, but the columns switched is okay. I.e., it's okay to have the first eigenvector in the last column of the last two matrices, and  be in the lower right hand corner of the second matrix.

First we find our eigenvalues by finding the characteristic equation, which is the determinant of  (or ).

Thus, we have eigenvalues of 4 and 2. Solving for the eigenvectors by finding the bases of the eigenspaces, we have

lambda = 4

Adding Row1 into Row 2, we're left with

So that 

And have an eigenvector of .

For lambda = 2, we have 

Adding -1 Row 1 into Row 2, we have

So that 

and  is an eigenvector.

Constructing our diagonalized matrix, we have 

Using the formula for calculating the inverses of 2x2 matrices, we have

To calculate the matrix exponential, we can just find the matrix exponential of  and multiply  and  back in. So .

 is just found by taking the entries on the diagonal and exponentiating. Thus, 

Multiplying together, we get