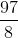We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Differential Equations : Differential Equations

Study concepts, example questions & explanations for Differential Equations

Create An Account

All Differential Equations Resources

1 Diagnostic Test 29 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : Numerical Solutions Of Ordinary Differential Equations

Use Euler's Method to calculate the approximation of y(0.2) where y(x) is the solution of the initial-value problem that is as follows.

y''+xy'+y=0

y(0)=2, y'(0)=3

Possible Answers:

$y(0.2)\approx2.584$

$y(0.2)\approx2.458$

$y(0.2)\approx2.5$

$y(0.2)\approx2.542$

$y(0.2)\approx2.58$

Correct answer:

$y(0.2)\approx2.58$

Explanation:

Using Euler's Method for the function

y''+xy'+y=0

y(0)=2, y'(0)=3

first make the substitution of

$\\y'=u \\u'=-xu-y$

therefore

$\\y_{n+1}=y_n+hu_n \\u_{n+1}=u_n+h[-x_nu_n-y_n]$

where represents the step size.

Let

$\\h=0.1 \\y_0=2 \\u_0=3$

Substitute these values into the previous formulas and continue in this fashion until the approximation for y(0.2) is found.

$\\y_1=y_0+(0.1)u_0=2+(0.1)(3)=2.3 \\u_1=u_0+(0.1)[-x_0u_0-y_0]=3+(0.1)[0(2)-2]=2.8 \\y_2=y_1+(0.1)u_1=2.3+(0.1)(2.8)=2.58 \\u_2=u_1+(0.1)[-x_1u_1-y_1]=2.8+(0.1)[-0.1(2.8)-2.3]=2.542$

Therefore,

$y(0.2)\approx2.58$

Report an Error

Example Question #2 : Euler Method

Use the implicit Euler method to approximate y(3) for y' = 5y , given that y(0) = 4 , using a time step of h = 1.

Possible Answers:

$-\frac{1}{16}$

$\frac{1}{32}$

$\frac{1}{16}$

Correct answer:

$-\frac{1}{16}$

Explanation:

In the implicit method, the amount to increase is given by $h \cdot f(t_{i+1}, y_{i+1})$ , or in this case $\mu_i = \mu_{i-1}+ 1 \cdot (5\mu_i)$ . Note, you can't just plug in to this form of the equation, because it's implicit: $\mu_i$ is on both sides. Thankfully, this is an easy enough form that you can solve explicitly. Otherwise, you would have to use an approximation method like newton's method to find $\mu_i$ . Solving explicitly, we have $-4\mu_i = \mu_{i-1}$ and $\mu_i = -\frac{\mu_{i-1}}{4}$ .

Thus, $y(1) \approx \mu_1 = -\frac{4}{4} = -1$

$y(2) \approx \mu_2 = -\frac{-1}{4} = \frac{1}{4}$

$y(3) \approx \mu_3 = -\frac{\frac{1}{4}}{4} = -\frac{1}{16}$

Thus, we have a final answer of $-\frac{1}{16}$

Report an Error

Example Question #1 : Numerical Solutions Of Ordinary Differential Equations

Use two steps of Euler's Method with h=0.1 on

$y' = x\sqrt{y} \ \ \ y(1) = 4$

To three decimal places

Possible Answers:

4.413

4.420

4.428

4.408

4.425

Correct answer:

4.425

Explanation:

Euler's Method gives us

$y_{n+1} = y_n + hf(x_n,y_n) = y_n + (0.1)x_n\sqrt{y_n}$

Taking one step

$y_1 = y_0 + (0.1)x_0\sqrt{y_0} = 4 + (0.1)(1)\sqrt{4} = 4.2$

Taking another step

$y_2 = y_1 + (0.1)x_1\sqrt{y_1} = 4.2 + (0.1)(1.1)\sqrt{4.2} \approx 4.425$

Report an Error

Example Question #1 : Multi Step Methods

The two-step Adams-Bashforth method of approximation uses the approximation scheme $y_{i+2} = y_{i+1} - \frac{1}{2}hf(t_i, y_i) + \frac{3}{2}hf(t_{i+1}, y_{i+1})$ .

Given that 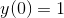y(0) = 1 and y(1) = 2 , use the Adams-Bashforth method to approximate y(3) for y = -y^2 with a step size of h = 1.

Possible Answers:

$\frac{55}{8}$

$\frac{33}{4}$

$\frac{133}{8}$

$-\frac{159}{8}$

$\frac{97}{8}$

Correct answer:

$-\frac{159}{8}$

Explanation:

In this problem, we're given two points, so we can start plugging in immediately. If we were not, we could approximate $y_{i+1}$ by using the explicit Euler method on $y_{i}$ .

Plugging into 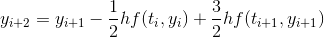$y_{i+2} = y_{i+1} - \frac{1}{2}hf(t_i, y_i) + \frac{3}{2}hf(t_{i+1}, y_{i+1})$ , we have

$y(2) \approx \mu_2 = 2 -\frac{1}{2}\cdot 1 \cdot -1^2 + \frac{3}{2}\cdot 1 \cdot -2^2 = 2 +\frac{1}{2} - 6 = -\frac{7}{2}$

$y(3)\approx \mu_3 = -\frac{7}{2} + \frac{1}{2}\cdot4 - \frac{3}{2}\cdot \frac{49}{4} =-\frac{159}{8}$ .

Note, our approximation likely won't be very good with such large a time step, but the process doesn't change regardless of the accuracy.

$y(3)\approx -\frac{159}{8}$

Report an Error

Example Question #1 : Second Order Boundary Value Problems

Find the solutions to the second order boundary-value problem. y'' -2y' + 2y = 0 , y(0) = 0 , $y\left(\frac{\pi}{2}\right) = 1$ .

Possible Answers:

$y = 5e^t\sin(t) + 3e^t\cos(t)$

$y = 10e^{2t}\sin(2t)$

There are no solutions to the boundary value problem.

$y = e^{t}\sin(t) - e^t\cos(t)$

$y = e^{t -\frac{\pi}{2}}\sin(t)$

Correct answer:

$y = e^{t -\frac{\pi}{2}}\sin(t)$

Explanation:

The characteristic equation of y'' -2y' + 2y = 0 is $\lambda^2 - 2\lambda + 2 = 0$ , with solutions of $\frac{2 \pm \sqrt{4 - 8}}{2} = 1 \pm i$ . Thus, the general solution to the homogeneous problem is $y = c_1e^t\sin(t) + c_2e^t\cos(t)$ . Plugging in our conditions, we find that y(0) = c_2 = 0 , so that $y = c_1e^t\sin(t)$ . Plugging in our second condition, we find that $y\left(\frac{\pi}{2}\right) = c_1e^{\frac{\pi}{2}} = 1$ and that $c_1 = e^{-\frac{\pi}{2}}$ .

Thus, the final solution is $y = e^{t -\frac{\pi}{2}}\sin(t)$ .

Report an Error

Example Question #2 : Second Order Boundary Value Problems

Find the solutions to the second order boundary-value problem. y'' + 9y = 0 , y(0) = 0 , $y\left(2\pi\right) = 1$ .

Possible Answers:

$y = 3\cos(3t)$

$y = 4\sin(3t) - \cos(3t)$

$y = 3\sin(3t)$

There are no solutions to the boundary value problem.

$y = \sin(3t) + 2 \cos(3t)$

Correct answer:

There are no solutions to the boundary value problem.

Explanation:

The characteristic equation of y'' + 9y = 0 is $\lambda^2 + 9 = 0$ with solutions of $\pm 3i$ . This tells us that the solution to the homogeneous equation is $y = c_1\sin(3t) + c_2\cos(3t)$ . Plugging in our conditions, we find that y(0) = c_2 = 0 so that $y = c_1\sin(3t)$ . Plugging in our second condition, we have $y(2\pi) = 0 = 1$ which is obviously false.

This problem demonstrates the important distinction between initial value problems and boundary value problems: Boundary value problems don't always have solutions. This is one such case, as we can't find c_1, c_2 that satisfy our conditions.

Report an Error

Example Question #1 : System Of Linear First Order Differential Equations

Find the general solution to the given system.

$\\\frac{dx}{dt}=x+2y \\\\\frac{dy}{dt}=2x+y$

Possible Answers:

$X=c_1\binom{1}{-1}e^{3t}+c_2\binom{-1}{3}e^{-t}$

$X=c_1\binom{1}{3}e^{3t}+c_2\binom{1}{1}e^{-t}$

$X=c_1\binom{1}{1}e^{3t}+c_2\binom{-1}{3}e^{-t}$

$X=c_1\binom{1}{1}e^{3t}+c_2\binom{1}{3}e^{-t}$

$X=c_1\binom{-1}{1}e^{3t}+c_2\binom{1}{3}e^{-t}$

Correct answer:

$X=c_1\binom{1}{1}e^{3t}+c_2\binom{-1}{3}e^{-t}$

Explanation:

To find the general solution to the given system

$\\\frac{dx}{dt}=x+2y \\\\\frac{dy}{dt}=2x+y$

first find the eigenvalues and eigenvectors.

$det(A-\lambda I )=\begin{vmatrix} 1-\lambda&2 \\ 2&1-\lambda \end{vmatrix}$

$\\=(1-\lambda)(1-\lambda)-(2)(2) \\=1-2\lambda+\lambda^2-4 \\=\lambda^2-2\lambda-3 \\=(\lambda-3)(\lambda+1)$

Therefore the eigenvalues are

$\lambda_1=3, \lambda_2=-1$

Now calculate the eigenvectors

$(A-\lamda I)K=0$

For

$\lambda_1=3$

$\\(1-3)k_1+2k_2 \\2k_1+(1-3)k_2$

Thus,

$k_1=k_2 \rightarrow K_1\binom{1}{1}$

For

$\lambda_1=-1$

$\\(2--1)k_1+1k_2 \\1k_1+(2--1)k_2$

Thus

$k_1=-\frac{1}{3}k_2\rightarrow K_2\binom{-1}{3}$

Therefore,

$X_1=\binom{1}{1}e^{3t};\ X_2\binom{-1}{3}e^{-t}$

Now the general solution is,

$\\X=c_1X_1+c_2X_2 \\\\X=c_1\binom{1}{1}e^{3t}+c_2\binom{-1}{3}e^{-t}$

Report an Error

Example Question #1 : Homogeneous Linear Systems

Solve the initial value problem $\mathbf{x'} = \begin{bmatrix} 3&-2 \\ -1&2 \end{bmatrix}\mathbf{x}$ . Where $\mathbf{x}_0 = \begin{bmatrix} 1\\-1 \end{bmatrix}$

Possible Answers:

$\mathbf{x} = e^t\begin{bmatrix} 3\\1 \end{bmatrix} +e^{4t}\begin{bmatrix} 5\\6 \end{bmatrix}$

$\mathbf{x} = e^{-t}\begin{bmatrix} 5\\2 \end{bmatrix} +e^{3t}\begin{bmatrix} -1\\3 \end{bmatrix}$

$\mathbf{x} = e^{-t}\begin{bmatrix} -2\\1 \end{bmatrix} +e^{3t}\begin{bmatrix} 2\\2 \end{bmatrix}$

$\mathbf{x} = e^t\begin{bmatrix} -3\\-3 \end{bmatrix} +e^{4t}\begin{bmatrix} 4\\2 \end{bmatrix}$

$\mathbf{x} = e^t\begin{bmatrix} 1\\4 \end{bmatrix} +e^{4t}\begin{bmatrix} 5\\2 \end{bmatrix}$

Correct answer:

$\mathbf{x} = e^t\begin{bmatrix} -3\\-3 \end{bmatrix} +e^{4t}\begin{bmatrix} 4\\2 \end{bmatrix}$

Explanation:

To solve the homogeneous system, we will need a fundamental matrix. Specifically, it will help to get the matrix exponential. To do this, we will diagonalize the matrix. First, we will find the eigenvalues which we can do by calculating the determinant of $\lambda I - A$ .

$|\lambda I - A| = \begin{vmatrix} \lambda - 3&2 \\ 1&\lambda - 2 \end{vmatrix} = (\lambda -3)(\lambda -2) - 2 = \lambda^2 - 5\lambda +4 = (\lambda -4)(\lambda -1)$

Finding the eigenspaces, for lambda = 1, we have

$\begin{bmatrix} -2&2 &\vline &0 \\ 1&-1 &\vline & 0 \end{bmatrix}$

Adding -1/2 Row 1 to Row 2 and dividing by -1/2, we have $\begin{bmatrix} 1&-1 &\vline &0 \\ 0&0 &\vline & 0 \end{bmatrix}$ which means x_1 + x_2 = 0

Thus, we have an eigenvector of $\begin{bmatrix} 1\\1 \end{bmatrix}$ .

For lambda = 4

$\begin{bmatrix} 1&-2 &\vline &0 \\ -1&2 &\vline & 0 \end{bmatrix}$

Adding Row 1 to Row 2, we have

$\begin{bmatrix} 1&-2 &\vline &0 \\ 0&0 &\vline & 0 \end{bmatrix}$

So x_1 - 2x_2 = 0 with an eigenvector $\begin{bmatrix} 2\\1 \end{bmatrix}$ .

Thus, we have $P = \begin{bmatrix} 1&2 \\ 1&1 \end{bmatrix}$ and $D = \begin{bmatrix} 1&0 \\ 0&4 \end{bmatrix}$ . Using the inverse formula for 2x2 matrices, we have that $P^{-1} = \begin{bmatrix} -1&2 \\ 1&-1 \end{bmatrix}$ . As we know that $e^{tA} = Pe^{tD}P^{-1}$ , we have $e^{tA} = \begin{bmatrix} 1&2 \\ 1&1 \end{bmatrix}\begin{bmatrix} e^t&0 \\ 0&e^{4t} \end{bmatrix}\begin{bmatrix} -1&2 \\ 1&-1 \end{bmatrix}= \begin{bmatrix} -e^t + 2e^{4t}&2e^{t} -2e^{4t} \\ -e^t + e^{4t}&2e^t-e^{4t} \end{bmatrix}$

The solution to a homogenous system of linear equations is simply to multiply the matrix exponential by the intial condition. For other fundamental matrices, the matrix inverse is needed as well.

Thus, our final answer is $\begin{bmatrix} -e^t + 2e^{4t}&2e^{t} -2e^{4t} \\ -e^t + e^{4t}&2e^t-e^{4t} \end{bmatrix}\begin{bmatrix} 1\\-1 \end{bmatrix} = \begin{bmatrix} -3e^t + 4e^{4t}\\-3e^t + 2e^{4t} \end{bmatrix}= e^t\begin{bmatrix} -3\\-3 \end{bmatrix} +e^{4t}\begin{bmatrix} 4\\2 \end{bmatrix}$

Report an Error

Example Question #1 : Homogeneous Linear Systems

Solve the homogenous equation:

y''-6y'+8y=0

With the initial conditions:

y(0)=2

y'(0)=5

Possible Answers:

$y(t)=C_{1}e^{-4t}+C_{2}e^{-2t}$

none of these answers

$y(t)=\frac{e^{-4t}}{2}+\frac{3e^{-2t}}{2}$

$y(t)=\frac{e^{4t}}{2}+\frac{3e^{2t}}{2}$

$y(t)=C_{1}e^{4t}+C_{2}e^{2t}$

Correct answer:

$y(t)=\frac{e^{4t}}{2}+\frac{3e^{2t}}{2}$

Explanation:

So this is a homogenous, second order differential equation. In order to solve this we need to solve for the roots of the equation. This equation can be written as:

r^2-6r+8=0 Which, using the quadratic formula or factoring gives us roots of $r_{1}=4$ and $r_{2}=2$

The solution of homogenous equations is written in the form:

$y(t)=C_{1}e^{r_{1}t}+C_{2}e^{r_{2}t}$ so we don't know the constants, but can substitute the values we solved for the roots:

$y(t)=C_{1}e^{4t}+C_{2}e^{2t}$

We have two initial values, one for y(t) and one for y'(t), both with t=0\

So:

$y(0)=2=C_{1}+C_{2}$

$y'(t)=4C_{1}e^{4t}+2C_{2}e^{2t}$ so: $y'(0)=5=4C_{1}+2C_{2}$

We can solve for $C_{2}$ : $2-C_{1}=C_{2}$ Then plug into the other equation to solve for $C_{1}$

$5=4C_{1}+2(2-C_{1})=4C_{1}+4-2C_{1}=2C_{1}+4$

So, solving, we get: $C_{1}=\frac{1}{2}$ Then $C_2=\frac{3}{2}$

This gives a final answer of:

$y(t)=\frac{e^{4t}}{2}+\frac{3e^{2t}}{2}$

Report an Error

Example Question #2 : System Of Linear First Order Differential Equations

Solve the second order differential equation:

3y''-3y'-6y=0

Subject to the initial values:

y(0)=4

y'(0)=2

Possible Answers:

none of these answers

$y(t)=2e^{2t}+2e^{-t}$

$y(t)=3e^{2t}+e^{-t}$

$y(t)=2e^{2t}-2e^{-t}$

$y(t)=3e^{2t}-e^{-t}$

Correct answer:

$y(t)=2e^{2t}+2e^{-t}$

Explanation:

So this is a homogenous, second order differential equation. In order to solve this we need to solve for the roots of the equation. This equation can be written as:

3r^2-3r-6=0 Which, using the quadratic formula or factoring gives us roots of $r_{1}=2$ and $r_{2}=-1$

The solution of homogenous equations is written in the form:

$y(t)=C_{1}e^{r_{1}t}+C_{2}e^{r_{2}t}$ so we don't know the constants, but can substitute the values we solved for the roots:

$y(t)=C_{1}e^{2t}+C_{2}e^{-t}$

We have two initial values, one for y(t) and one for y'(t), both with t=0

So:

$y(0)=4=C_{1}+C_{2}$

$y'(t)=2C_{1}e^{2t}-C_{2}e^{-t}$ so: $y'(0)=2=2C_{1}-C_{2}$

We can solve $4-C_{1}=C_{2}$ Then plug into the other equation to solve for $C_{1}$

$2=2C_{1}-(4-C_{1})=2C_{1}+C_{1}-4=3C_{1}-4$

So, solving, we get: $C_{1}=2$ Then C_2=2

This gives a final answer of:

$y(t)=2e^{2t}+2e^{-t}$

Report an Error

View Differential Equations Tutors

Dereika
Certified Tutor

Southern University and A & M College, Bachelor of Science, Accounting. Grand Canyon University, Master of Science, Accounting.

View Differential Equations Tutors

Reza
Certified Tutor

University of Sherbrooke, Doctor of Philosophy, Mathematics. University of Manitoba, Master of Science, Mathematics.

View Differential Equations Tutors

Robert
Certified Tutor

Rensselaer Polytechnic Institute, Bachelors, Electrical Engineering. Brooklyn Polytechnic, Masters, Computer Science.

All Differential Equations Resources

1 Diagnostic Test 29 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ACT Tutors in Chicago, Chemistry Tutors in New York City, SSAT Tutors in Phoenix, Physics Tutors in Dallas Fort Worth, ACT Tutors in Denver, Computer Science Tutors in Houston, Calculus Tutors in Chicago, SSAT Tutors in Boston, LSAT Tutors in Miami, GRE Tutors in San Francisco-Bay Area

Popular Courses & Classes

GRE Courses & Classes in Boston, ISEE Courses & Classes in Miami, ACT Courses & Classes in Philadelphia, MCAT Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Atlanta, SSAT Courses & Classes in Washington DC, ACT Courses & Classes in Chicago, ACT Courses & Classes in Atlanta, LSAT Courses & Classes in Chicago, GMAT Courses & Classes in Chicago

Popular Test Prep

SSAT Test Prep in Seattle, ISEE Test Prep in San Francisco-Bay Area, GRE Test Prep in Washington DC, ISEE Test Prep in San Diego, ACT Test Prep in Chicago, MCAT Test Prep in New York City, GMAT Test Prep in Seattle, GRE Test Prep in Phoenix, ACT Test Prep in Atlanta, SSAT Test Prep in Los Angeles

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Differential Equations : Differential Equations

Study concepts, example questions & explanations for Differential Equations

All Differential Equations Resources

Example Questions

Example Question #2 : Numerical Solutions Of Ordinary Differential Equations

Example Question #2 : Euler Method

Example Question #1 : Numerical Solutions Of Ordinary Differential Equations

Example Question #1 : Multi Step Methods

Example Question #1 : Second Order Boundary Value Problems

Example Question #2 : Second Order Boundary Value Problems

Example Question #1 : System Of Linear First Order Differential Equations

Example Question #1 : Homogeneous Linear Systems

Example Question #1 : Homogeneous Linear Systems

Example Question #2 : System Of Linear First Order Differential Equations

All Differential Equations Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: