All Common Core: High School - Geometry Resources
Example Questions
Example Question #2 : Cylinders, Pyramids, Cones, And Spheres Volume Formulas: Ccss.Math.Content.Hsg Gmd.A.3
Find the radius of a hemisphere, where the volume is
Round your answer to 
Before we find the radius of a hemisphere, we need to recall the equation.
Since we are given the volume (
Now we can solve for 
Now we divide by
Now our equation is
To solve for 
Here is a picture representation of the hemisphere.

Example Question #4 : Cylinders, Pyramids, Cones, And Spheres Volume Formulas: Ccss.Math.Content.Hsg Gmd.A.3
Find the radius of a hemisphere, where the volume is 
Round your answer to 
Before we find the radius of a hemisphere, we need to recall the equation.
Since we are given the volume (
Now we can solve for 
Now we divide by 
Now our equation is
To solve for 
Here is a picture of what the hemisphere look like.

Example Question #2 : Cylinders, Pyramids, Cones, And Spheres Volume Formulas: Ccss.Math.Content.Hsg Gmd.A.3
Find the radius of a hemisphere, where the volume is 
Round your answer to 
Before we find the radius of a hemisphere, we need to recall the equation.
Since we are given the volume (
Now we can solve for 
Now we divide by 
Now our equation is
To solve for 
Here is a picture of the hemisphere.

Example Question #1 : Cylinders, Pyramids, Cones, And Spheres Volume Formulas: Ccss.Math.Content.Hsg Gmd.A.3
Find the radius of a sphere, where the volume is 
Round your answer to 
Before we find the radius of a sphere, we need to recall the equation.
Since we are given the volume (
Now we can solve for 
Now we divide by 
Now our equation is
To solve for 
Here is a picture of the sphere.

Example Question #41 : Geometric Measurement & Dimension
Find the radius of a sphere, where the volume is 
Round your answer to 
Before we find the radius of a sphere, we need to recall the equation.
Since we are given the volume (
Now we can solve for 
Now we divide by 
Now our equation is
To solve for 
Here is a picture of the sphere.

Example Question #42 : Geometric Measurement & Dimension
Find the radius of a hemisphere, where the volume is 
Round your answer to 
Before we find the radius of a hemisphere, we need to recall the equation.
Since we are given the volume (
Now we can solve for 
Now we divide by 
Now our equation is
To solve for 
Here is a picture of the hemisphere.

Example Question #1 : Identify Shapes In 2 D Cross Sections And Rotations In 3 D: Ccss.Math.Content.Hsg Gmd.B.4
Given a cylinder with radius 

The first step is see what the cross section parallel to the base looks like.
Since we are dealing with a cylinder, the cross section that we are dealing with parallel to the base is a circle.
So all we need to do is recall the area of a circle equation, and substitute the radius given for 
Now we round our answer to the nearest tenth
Example Question #2 : Identify Shapes In 2 D Cross Sections And Rotations In 3 D: Ccss.Math.Content.Hsg Gmd.B.4
Given a sphere with a volume of 
The first step is to recall the volume equation of a sphere.
Since we are given the volume, we can plug it in for V
Since we want to find the area of the perpendicular cross section, we need to find what the radius is.
Now we solve for
Now we can use the radius we found to find the area of the cross section.
The cross section in this case is a circle, so now we will use the area of a circle formula, which is
Now we simply substitute the radius we just found for 
Now we round our answer to the nearest tenth, which is
Example Question #1 : Identify Shapes In 2 D Cross Sections And Rotations In 3 D: Ccss.Math.Content.Hsg Gmd.B.4
Given a sphere with a volume of 
The first step is to recall the volume equation of a sphere.
Since we are given the volume, we can plug it in for V
Since we want to find the area of the perpendicular cross section, we need to find what the radius is.
Now we solve for r
Now we can use the radius we found to find the area of the cross section.
The cross section in this case is a circle, so now we will use the area of a circle formula, which is
Now we simply substitute the radius we just found for 
Now we round our answer to the nearest tenth, which is
Example Question #411 : High School: Geometry
Given a sphere with a volume of 
The first step is to recall the volume equation of a sphere.
Since we are given the volume, we can plug it in for V
Since we want to find the area of the perpendicular cross section, we need to find what the radius is.
Now we solve for r
Now we can use the radius we found to find the area of the cross section.
The cross section in this case is a circle, so now we will use the area of a circle formula, which is
Now we simply substitute the radius we just found for 
Now we round our answer to the nearest tenth, which is
Certified Tutor
Certified Tutor
All Common Core: High School - Geometry Resources























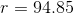















































![\\7323 = \pi r^{3} \\\\\frac{7323}{\pi} = r^{3} \\r=\sqrt[3]{ \frac{7323}{\pi} }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1052309/gif.latex)










![\\6354 = \pi r^{3} \\\\\frac{6354}{\pi} = r^{3} \\r=\sqrt[3]{ \frac{6354}{\pi} }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1052290/gif.latex)










![\\3843 = \pi r^{3} \\\\\frac{3843}{\pi} = r^{3} \\r=\sqrt[3]{ \frac{3843}{\pi} }](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1052297/gif.latex)






