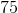All Common Core: 7th Grade Math Resources
Example Questions
Example Question #41 : Statistics & Probability
A teacher is comparing two students' median test scores, as show in the dot plots below. Which student had a higher median score, and what was this student's median score?


Student B-
Student A-
Student B-
Student A-
Student A-
The median is the middle number of a set of data points.
To solve for the median, we list our data points in order from least to greatest, and then find the number in the middle.
Student A:
Student B:
Student A has the higher median score,
Example Question #42 : Statistics & Probability
A teacher is comparing two students' median test scores, as show in the dot plots below. Which student had a higher median score, and what was this student's median score?


Student B-
Student A-
Student B-
Student A-
Student B-
The median is the middle number of a set of data points.
To solve for the median, we list our data points in order from least to greatest, and then find the number in the middle.
Student A:
Student B:
Student B has the higher median score,
Example Question #11 : Use Measure Of Center And Measure Of Variability To Compare Populations: Ccss.Math.Content.7.Sp.B.4
A teacher is comparing two students' median test scores, as show in the dot plots below. Which student had a higher median score, and what was this student's median score?


Student A-
Student A-
Student B-
Student B-
Student B-
The median is the middle number of a set of data points.
To solve for the median, we list our data points in order from least to greatest, and then find the number in the middle.
Student A:
Student B:
Student B has the higher median score,
Example Question #12 : Use Measure Of Center And Measure Of Variability To Compare Populations: Ccss.Math.Content.7.Sp.B.4
A teacher is comparing two students' median test scores, as shown in the dot plots below. Which student had a higher median score, and what was this student's median score?


Student B-
Student A-
Student B-
Student A-
Student B-
The median is the middle number of a set of data points.
To solve for the median, we list our data points in order from least to greatest, and then find the number in the middle.
Student A:
Student B:
Student B has the higher median score,
Example Question #43 : Statistics & Probability
Select the answer choice that has the greatest probability of occurring.
Using a standard deck of cards, drawing a 
Using a standard deck of cards, drawing a 
Using a standard deck of cards, drawing a 
Using a standard deck of cards, drawing a 
Using a standard deck of cards, drawing a 
Probability is represented by a number between 

Probabilities are usually written in a fraction form that expresses the likelihood of the event occurring. The greater the fraction—or number—then there is a better probability of the event occurring.
Each of our answer choices use a standard deck of cards, which has 
First, let's find the probability of each event:
Drawing a 

Drawing a 

Drawing a 

Drawing a 

This is the greatest probability and the correct answer.
Example Question #44 : Statistics & Probability
Select the answer choice that has the greatest probability of occurring.
Using a standard deck of cards, drawing a King
Using a standard deck of cards, drawing the King of Hearts
Using a standard deck of cards, drawing a black King
Using a standard deck of cards, drawing a red King
Using a standard deck of cards, drawing a King
Probability is represented by a number between 

Probabilities are usually written in a fraction form that expresses the likelihood of the event occurring. The greater the fraction—or number—then there is a better probability of the event occurring.
Each of our answer choices use a standard deck of cards, which has 
First, let's find the probability of each event:
Drawing the King of Hearts : There is only one King of Hearts in a standard deck; thus, the probability is:
Drawing a black King: There are two black Kings in a standard deck; thus, the probability is:
drawing a red King: There are two red Kings in a standard deck; thus, the probability is:
Drawing a King: There are four Kings in a standard deck; thus, the probability is:
This is the greatest probability and the correct answer.
Example Question #45 : Statistics & Probability
Select the answer choice that has the greatest probability of occurring.
Using a standard deck of cards, drawing a red 
Using a standard deck of cards, drawing a
Using a standard deck of cards, drawing a face card
Using a standard deck of cards, drawing an ace
Using a standard deck of cards, drawing a face card
Probability is represented by a number between 

Probabilities are usually written in a fraction form that expresses the likelihood of the event occurring. The greater the fraction—or number—then there is a better probability of the event occurring.
Each of our answer choices use a standard deck of cards, which has 
First, let's find the probability of each event:
Drawing a red 

Drawing a 

Drawing an ace: There four aces in a standard deck; thus, the probability is:
Drawing a face card: There are 



This is the greatest probability and the correct answer.
Example Question #4 : Understand Probability Of A Chance Event: Ccss.Math.Content.7.Sp.C.5
Select the answer choice that has the lowest probability of occurring.
Using a standard deck of cards, drawing a face card
Using a standard deck of cards, drawing a red 
Using a standard deck of cards, drawing an ace
Using a standard deck of cards, drawing a
Using a standard deck of cards, drawing a red 
Probability is represented by a number between 

Probabilities are usually written in a fraction form that expresses the likelihood of the event occurring. The greater the fraction—or number—then there is a better probability of the event occurring.
Each of our answer choices use a standard deck of cards, which has 
First, let's find the probability of each event:
Drawing a 

Drawing an ace: There four aces in a standard deck; thus, the probability is:
Drawing a face card: There are 



Drawing a red 

This is the lowest probability and the correct answer.
Example Question #5 : Understand Probability Of A Chance Event: Ccss.Math.Content.7.Sp.C.5
Select the answer choice that has the greatest probability of occurring.
Using a standard deck of cards, drawing an ace
Using a standard deck of cards, drawing a face card
Using a standard deck of cards, drawing a red card
Using a standard deck of cards, drawing a red
Using a standard deck of cards, drawing a red card
Probability is represented by a number between 

Probabilities are usually written in a fraction form that expresses the likelihood of the event occurring. The greater the fraction—or number—then there is a better probability of the event occurring.
Each of our answer choices use a standard deck of cards, which has 
First, let's find the probability of each event:
Drawing a red 

Drawing an ace: There 
Drawing a face card: There are 



Drawing a red card : Half of the cards in a standard deck are red; thus, the probability is:
This is the greatest probability and the correct answer.
Example Question #6 : Understand Probability Of A Chance Event: Ccss.Math.Content.7.Sp.C.5
Select the answer choice that has the lowest probability of occurring.
Using a standard deck of cards, drawing a red card
Using a standard deck of cards, drawing a face card
Using a standard deck of cards, drawing a red
Using a standard deck of cards, drawing an ace
Using a standard deck of cards, drawing a red
Probability is represented by a number between 

Probabilities are usually written in a fraction form that expresses the likelihood of the event occurring. The greater the fraction—or number—then there is a better probability of the event occurring.
Each of our answer choices use a standard deck of cards, which has 
First, let's find the probability of each event:
Drawing an ace: There 
Drawing a face card: There are 



Drawing a red card : Half of the cards in a standard deck are red; thus, the probability is:
Drawing a red 

This is the lowest probability and the correct answer.
All Common Core: 7th Grade Math Resources