All College Physics Resources
Example Questions
Example Question #4 : Conservation Of Momentum And Energy
If an object has a kinetic energy of 


Let's first write down the information we are given:
In order to solve this problem we must apply the conservation of energy, which states 
This means that as the project reaches its max height energy is converted from Kinetic energy (energy of motion) to potential gravitational energy (based off of height).
We can subtract 



so we can solve for the mass
where
therefore
Example Question #2 : Mechanics
A 


The formula for gravitational potential energy is:
To find the potential energy lost, we need to find the potential energy of the ball at two heights, then find the difference.
Note that the energy was not actually lost; rather, it was converted to kinetic energy.
Example Question #1 : Work And Energy
A baseball weighing 

Gravitational potential energy is given by the equation:
We are given all the information needed to solve for the potential energy.
Plug in known values and solve.
Recall that the units for energy are Joules. Newtons is the unit for force.
Example Question #3 : Mechanics
A 

The equation for gravitational potential energy is:
We are given all the information needed to answer the question.
Plug in known values and solve.
Example Question #21 : College Physics
Suppose that an object of mass 


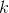
Note: Assume that there is no friction.
For this question, we're told than an object is travelling with a certain velocity towards a spring. After colliding with the spring and causing it to undergo a maximum displacement, we're asked to provide an expression for the spring constant.
In order to answer this question, we'll need to consider the energy of the object and the spring during the process described. First, the object is moving with a certain velocity towards the spring. Thus, the object has kinetic energy. When the object collides with the spring and displaces the spring to its maximum displacement, there will be a brief instant where the object has completely stopped moving. At this point, all of the block's kinetic energy will have been transferred into the spring in the form of potential energy. With this information in mind, we can equate the two forms of energy.
Now, we can rearrange terms in order to isolate 
Example Question #1 : Motion In Two Dimensions
A rock is tossed horizontally off the edge of a cliff with a velocity of 

This question requires an understanding of motion in two dimensions. The most important concept in this question is that the motion in each dimension is independent. Since the rock's initial velocity is purely in the horizontal direction, the initial velocity has no impact on the vertical velocity at any point. Likewise, the vertical acceleration has no impact on the horizontal speed. The rock will travel at 
To solve this problem, the first step is to set up an expression for the horizontal and vertical velocities as a function of time:
Thus,
Substituting 



Example Question #2 : Motion
A projectile reaches it max height in 

We first must find the initial vertical velocity (
We know that 
we also know that 
So plugging in what we know:
Knowing that 

Example Question #3 : Motion
If an object strikes the ground at 
First let's make a table of what we know:

It should also be noted it is simpler to define things so that the initial height is zero, so we don't have to deal with a bunch of negative numbers.
Also, since it is dropped vertically and we are only interested in the height it is dropped from we aren't interested in any information regarding the projectile's horizontal motion.
Let's use the equation:
since
We can solve for 
This is our final answer.
Example Question #4 : Motion
A projectile is launched vertically upwards at 
First let's write down the information we're given:


Let's use the equation
to solve for the time it takes the projectile to reach its max height.
Solving for 
Now lets plug in what we know and calculate the time:

Example Question #12 : Mechanics
A projectile is launched vertically upwards at 
First let's write down the information we're given:


Let's use the following equation to solve for the time it takes the projectile to reach its max height:
Solving for 
Now lets plug in what we know and calculate the time:
Since the projectile takes twice as long to land as its does to reach its max height we simply multiple the 


All College Physics Resources






















































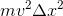





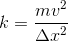








![speed_{total}=\sqrt{(5\frac{m}{s})^2+[(0.5)(9.81\frac{m}{s^2})t^2]^2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/956612/gif.latex)









































![\frac{(0-17)}{[-10]}=t=1.7s](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1002383/gif.latex)


