A conductor is defined as a object free to move charges. In particular, valence electrons, which are the outer most electron in each atom and the most free to move, travel inside the conductor until the net electric field inside the conductor is zero. These electrons will move until this condition has been met. Because of the presents of charged particles at the surface and the condition that they are no longer moving, any electric field at the surface must be perpendicular to that surface.

Gauss' laws states that the the electric flux through a Gaussian surface will be proportional to the net total charge inside the Gaussian surface. By inspection of the figure, we see that Gaussian surface B is the correct answer.

According to Gaussian law, the electric flux will be zero when the net electric charge inside the Gaussian surface is zero. By inspection, we see this is Gaussian surface C.

According to Gauss's law, the total electric flux is equal to the net total electric charge inside the a Gaussian surface. If the Gaussian surface is three times larger, the electric flux will be the same if both Gaussian surfaces contain the same amount of total electric charge.

The direction of electric field describes the trajectory of a positive test charge. Since a positive test charge would want to move away from the positive metal plate and towards the negative metal plate, the direction would be A.

The energy of a photon of a given frequency is determined by the equation

, where  is Plank's constant 

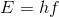
So plug in Plank's constant and the frequency of the x-ray photons to get an energy of very near 

This question requires no math to correctly answer! You should not need to 'brute force' it. Although it is designed to appear time consuming, it should be relatively easily once the principle of resistors in parallel is understood. Whenever two resistors are connected in parallel, the net resistance must be less than the resistance of either of the two alone. When resistors are connected in series, the net resistance must be more than the resistance of either alone.

Explanation of correct answer:

 and  in parallel, connected to  in series - It is possible to 'eyeball' this to see that this is at least feasible.  and  in parallel must make a network with an overall resistance less than . When added in series with  (), the overall may fall between  and . To confirm, one could do the math to calculate the overall resistance, but the point of this question is to use general principles to quickly eliminate the other, incorrect answer choices.

Explanations of incorrect answers:

, , and  in parallel - This combination cannot possibly work since the overall resistance must be less than  (the smallest resistor in parallel).

 and  in parallel, connected to  in series - Regardless of the overall resistance of  and  in parallel, the connection with  in series makes the total resistance more than .

 and  in parallel;  is not necessary - Placing  and  in parallel must result in a resistance less than .

, , and  in series - Connecting resistors in series results in an overall resistance greater than that of any one alone. Since  and  are included in series, the sum of the resistances is obviously much greater than what we are asked to produce and this choice can be immediately eliminated.

In this question, we're given a number of parameters of a circuit and are asked to find how we can use these various parameters to show the capacitance of the circuit's capacitor.

First, recall what a capacitor is; something that stores charge for a given voltage difference. In other words, when there is a voltage difference between the two plates of a capacitor, a certain amount of charge can be stored on these plates. The more charge that can be stored for a given voltage difference, the greater that capacitor's capacitance. This can be shown by the following equation.

From the above expression,  is the capacitance which we are trying to find a proper expression for.  is the charge accumulated on the plates, which is one parameter we're given. Voltage, , on the other hand, is not provided.

To put the voltage into different terms, we'll need to use Ohm's law, which states the following.

In other words, the voltage is proportional to both the current and the resistance of the circuit.

Since we are given both current and resistance as known parameters in the question stem, we can use these for our final answer. By substituting the  in the capacitance expression with , we obtain the following answer.

The capacitance of a parallel plate capacitor is proportional to the inverse of the distance between the plates. If the distance is halved, the capacitance is doubled.

The formula for finding the voltage of a simple RC circuit is 

, where  is the capacitor voltage,  is the source voltage,  is the resistance, and  is the capacitance.

We want to know when the capacitor will reach the voltage of the power source  so 

 and thus 

Using the properties of natural logs yields

Solving for  yields