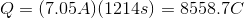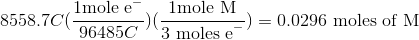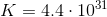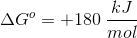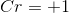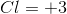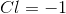All College Chemistry Resources
Example Questions
Example Question #1 : Redox Reactions
Suppose that the only elements a compound contains are carbon, hydrogen, and oxygen. If complete combustion of 




Note: The molecular weight of this compound is 
To answer this question, it's important to remember the details of combustion reactions. In the presence of oxygen and a sufficient amount of energy to initiate the process, combustion reactions that go to completion will result in the complete oxidation and breakdown of the initial reactant.
The 

The first step then is to use the mass of each product to find the mass of each element in the original compound. To do this, we'll need to use the molar mass for each of the products as well as the individual elements.
The combined mass of carbon and hydrogen in the original compound is 
The remaining mass will come from oxygen. Thus, the original compound will contain 
Once we have the mass of each element, we can use that information to calculate the number of moles of each element in the original compound.
Now that we have the relative molar amounts of each element in the original compound, we can find the empirical formula by finding the smallest whole number ratios.
From this, we can conclude that the empirical mass of the compound is 
Finally, since we are given the compound's molecular weight, we can use that information to find the molecular formula for the compound.
Example Question #1 : Reactions
Electrolysis of an unknown metal chloride, 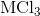
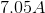
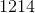
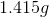
Titanium
Scandium
Chromium
Nickel
Titanium
Start by writing out the equation that illustrates the plating out of the metal:
Note the stoichiometric ratio for the moles of electrons to the moles of the metal.
Next, recall the following equation:
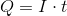



Plug in the given information to find 
Next, recall Faraday's law of electrolysis that equates Faraday's constant and the amount of electrons together to find the charge needed to deposit one mole of a particular substance.
Thus, we can set up the following to take the charge of the electrolysis through to figure out the number of moles unknown metal that was plated out.
Now, since we have the number of grams of the metal deposited, we can find the molar mass of the unknown metal.
The molar mass indicates that the metal must be titanium.
Example Question #1 : Reactions
Scandium can be plated out of a solution containing 
How many minutes would it take to plate out 

Recall the following formula:





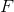
Start by finding how many moles of scandium was plated out.
Now, use the stoichiometric ratio present in the half reaction to find the number of moles of electrons.
Now, use the above formula to solve for the time.
Now, convert the seconds to minutes. Remember that your answer should only have 
Example Question #1 : Reactions
Consider the following redox reaction.
If 




In this question, we're given an overall redox reaction as well as the relevant reduction potentials, and we're asked to solve for 
To begin with, we can show each of the individual half reactions to make it more clear.
For gold:
For bromine:
Note that the reduction potential for each of these half reactions is positive. This means that for both elements, their reduction is spontaneous. The more positive the voltage (or the less negative), the more spontaneous it is.
From the overall question given to us in the question stem, we see that bromine is not being reduced but, rather, it is being oxidized. Since oxidation is the reverse of reduction, the reduction potential maintains the same magnitude but the sign in front of it changes. Thus, the oxidation of bromine has a value of 
To find the overall 
One very important thing to note is that we did not need to multiply the reduction potential for either of the half reactions. Even though the reduction reaction for gold needs two stoichiometric equivalents, and bromine's oxidation needs three stoichiometric equivalents, the values of 



Example Question #92 : College Chemistry
The standard reduction potential of silver is equal to 
Cobalt, with a standard reduction potential equal to
Copper, with a standard reduction potential equal to
Sodium, with a standard reduction potential of
Nickel, with a standard reduction potential of
Cobalt, with a standard reduction potential equal to
In this question, we're given the standard reduction potential of silver and told that it acts as the anode in a voltaic cell. We're then asked to identify a compound that could act as the cathode.
First, there are a few things we need to recognize. For one thing, we're told this is a voltaic cell, which hosts spontaneous redox reactions. This means that energy will be liberated from the reaction and, thus, the overall potential of the cell needs to be positive.
Moreover, the anode is the half-cell where oxidation occurs. In this case, since silver is serving as the anode, it is silver that will be oxidized. The electrons released from this oxidation will travel through the wire to the cathode, liberating energy available to do work in the process. Once at the cathode, the electron will be used to reduce whichever compound is at the cathode.
Since we're given the standard reduction potential of silver and we know the overall reaction must be spontaneous, we can determine what kind of reduction potential the cathode would need to have. Remember that in an electrochemical cell, the cell potential can be expressed as follows.
Moreover, as was mentioned previously, since this is a voltaic cell the reaction will be spontaneous and thus the 
Plugging in the value for 
This shows us that the cathode half-cell needs to have a compound with a standard reduction potential that is greater than silver's. The only answer choice that fits this criteria is cobalt, which has a standard reduction potential of 
Example Question #93 : College Chemistry
Consider the following redox reaction carried out in a voltaic cell.
If the reduction potential for 






For this question, we're given a redox reaction occurring within a voltaic cell. We're also supplied with the reduction potentials for the elements in the reaction, and are asked to find the standard free energy change as well as the equilibrium constant of the reaction at a given temperature.
Recall that in a voltaic cell, the reaction does not consume energy but rather produces it. The anode is where oxidation occurs, while the cathode is where reduction takes place. Based on the reaction given to us in the question stem, the anode will consist of solid 
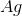




Knowing this, we can calculate 
Now that we have 
A couple things to note. The value for 

To find the value of 

Using 
Using 
As shown above, either method leads us to the same value for 
Example Question #92 : College Chemistry
Determine the oxidation number of each element in the compound
The oxidation number of each element in the compound 
The oxidation number of chlorine is 
Because this is a neutral atom, the overall charge is 0. Therefore we can set
Therefore,
We can then solve for the oxidation number for
Example Question #1 : Reactions
Given the following equation, identify the reducing agent.
Recall that a reducing agent is being oxidized and is losing electrons. Thus, when looking at the equation, look for which oxidation state is becoming more positive.
Start by assigning oxidation states to the elements.
For the reactants:







Now, assign the oxidation state of the products.








Only 
Example Question #93 : College Chemistry
In the given reaction, which element(s) is/are oxidized?


Let's start by looking at the equation and assigning oxidation numbers based off of the general rules we are given:
Let's start by looking at the reactants, namely 



Next let's look at 




so 

Now we have the oxidation numbers of all the elements present in this equation that are on the reactant side. I recommend writing down their oxidation numbers next to each other, so the elements that are oxidized and reduced can quickly be determined.
Oxidation numbers of elements in reactants:
Now let's look at the product side of the equation and determine the oxidation numbers of the elements there. First let's look at 







Finally, let's look 



Let's now write down the oxidation numbers of all the elements in the products.
Oxidation numbers of elements in products:
Now let's compare the oxidation numbers of the elements in the reactants with those in the products. 








Example Question #94 : College Chemistry
Which compound below has a nitrogen atom at a 
Let's start by going through each answer case-by-case applying the elementary rules of oxidation states we are given. The most applicable of these rules in this problem are the oxidation state of hydrogen in a compound is generally equal to 

Let's start by looking at 





solving for 



Let's still look at the other cases, however:
As this compound is uncharged we know it's net charge is equal to
Using our knowledge of oxidation states of hydrogen and oxygen and counting the number of hydrogens and oxygen in this compound, we can determine that the total charge of all the hydrogens together is equal to 

Just as we did above we can create an equation and solve for our unknown.
therefore 


Next let's look at 
We can quickly apply our knowledge of oxidation states of oxygen knowing that the oxidation state of oxygen in compounds is generally 



So our equation for this becomes:
therefore 

Finally the last compound is 
With this compound we can apply the rule we know about hydrogen's oxidation state in a compound being equal to 



Since there are two nitrogens, our equation is:
and 

Certified Tutor
All College Chemistry Resources