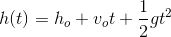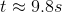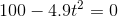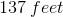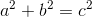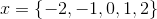1) The first step would be to simplify, but since 2, 15, and 25 have no common factors greater than 1, simplification is impossible.

Now we factor. Multiply the first coefficient by the final term and list off the factors.

2 * 25 = 50

Factors of 50 include:

1 + 50 = 51

2 + 25 = 27

5 + 10 = 15

2) Split up the middle term to make factoring by grouping possible.

Note that the "2" and the "10," and the "5" and the "25," have to go together for factoring to come out with integers. Always make sure the groups actually have a common factor to pull.

3) Pull out the common factors from both groups, "2x" from the first and "5" from the second.

4) Factor out the "(x+5)" from both terms.

5) Set each parenthetical expression equal to zero and solve.

2x + 5 = 0,  x = –5/2

x + 5 = 0, x = –5

The quadratic formula is as follows:

We will start by finding the values of the coefficients of the given equation:

Quadratic equations may be written in the following format:

In our case, the values of the coefficients are:

Substitute the coefficient values into the quadratic equation:

After simplifying we are left with:

leaving us with our two solutions:

 and 

To solve for x, we must first simplify the trinomial into two binomials.

To simplify the trinomial, its general form given by , we must find factors of  that when added give us . For our trinomial,  and the two factors that add together to get  are  and .

Now, using the two factors, we can rewrite  as the sum of the two factors each multiplied by x:

Next, we group the first two and last two terms together and factor each of the groups:

Now, simplify further:

Finally, set each of these binomials equal to zero and solve for x:

To solve for , we can use the quadratic formula:

Add 3 to both sides of the equation, to isolate the x terms: 

Divide each term by 8, to isolate the x² term: 

Add the square of one half of the "b" term to each side:

Simplify: 

Simplify further: 

Use the following factoring rule to simplify the left side of the equation: 

Take the square root of both sides of the equation: 

Simplify: 

Subtract one eighth from each side of the equation:  or 

Simplify the equations: 

Solution: 

In order to find the perimeter, start by defining the variables. It is typically easier to define one of the variables in terms of the other; therefore, only one unknown will need to be calculated to find the perimeter. The problem states that the length is eleven more than twice the width; thus, we can define our variables in the following way:

The farmer knows that the field's area is thirty square meters. Area is found using the following formula:

Substitute in the known value for the area and the defined variables for the length and width. 

Notice that this equation possesses all the components of a quadratic. Use the information in the equation to construct a quadratic equation that can be factored to obtain an answer. Start by multiplying the first term by the variable on the right side of the equation.

In order to make the quadratic equal to zero, subtract 30 from both sides of the equation. 

Now, factor the quadratic and solve for the variable. We can use the ac method to solve for the variable. Quadratics can be written in the following format:

We need to find two numbers whose product equals a multiplied by c and whose sum equals b; therefore, the product of the factors must be -60 and their sum must equal 11. Write out the prime factorization of 60.

There is one factor of -60 that when added together sum to equal 11: 15 and -4.

Use the factors and split the middle term in the quadratic in order to make factoring by grouping possible.

Pull the greatest common factor from each pair of terms:  from the first and 15 from the second.

Factor out the quantity  from both terms.

Set each factor equal to zero and solve for w.

We can cross out the this negative option because the width of a dimension cannot be a negative value. Solve for w in the second factor.

The width of the field is 2 meters. Substitute 2 in for the variable w and solve for the perimeter.

Perimeter is found using the formula:

The perimeter of the field is 34 meters.  

We're given the function,  

We know that the gravitational acceleration on earth is: 

 (meters-per-square second)

Because the ball starts at rest, the initial velocity  is zero, 

 (meters-per-second) 

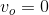
We are given the initial height, 

 (meters) 

When the ball reaches the ground, the height is "zero," so the value of  is zero at this time, and so we have: 

  (units omitted in the equation).

(Note that although taking the square root of both sides of an equation will produce positive and negative solutions, we ignore the negative solution since "negative time" makes no sense in the context of this problem).

Use Pythagorean Theorem to solve.

Since the path around the corner is 3x, 3 times the   is approximately 137. The distance saved is 137-102= 35 feet.  Note that we only needed the positive square root since we cannot have a negative distance.

To make this problem easier, lets start off by doing a u-substitution.

Let .

Now we can factor the left hand side.

We have two solutions for , now we can plug those into , to get all the solutions.

Find the roots of the polynomial, 

Set   equal to 

Factor out , 

Notice that the the factor  is a quadratic even though it might not seem so at first glance. One way to think of this is as follows: 

Let 

Then we have ,  substitute into  to get, 

Notice that the change in variable from  to  has resulted in a quadratic equation that can be easily factored due to the fact that it is a square of a simple binomial: 

The solution for  is, 

Because  we go back to the variable , 

Therefore, the roots of the   factor are, 

The other root of  is  since the function clearly equals  when . 

The solution set is therefore, 

Below is a plot of . You can see where the function intersects the -axis at points corresponding to our solutions. 

Further Discussion 

The change of variable was a tool we used to write the quadratic factor in a more familiar form, but we could have just factored the original function in terms of  as follows, 

Setting this to zero gives the same solution set,