All College Algebra Resources
Example Questions
Example Question #471 : College Algebra
Give the complete solution set for the equation:
can be rewritten in quadratic form by setting 

By the reverse-FOIL method we can factor the trinomial at left. We are looking for two integers with sum 8 and product 12; they are 2 and 6, so the equation becomes
Setting both binomials equal to 0, it follows that


Substituting 


in which case

or
in which case

The solution set is 
Example Question #471 : College Algebra
Give the complete set of real solutions for the equation:
The equation has no solutions.
can be rewritten in quadratic form by setting 

By the reverse-FOIL method we can factor the trinomial at left. We are looking for two integers with sum 8 and product 12; they are 

Setting both binomials equal to 0, it follows that


Substituting 

in which case

and

in which case
The set of real solutions is therefore 
Example Question #473 : College Algebra
Solve for 
There are no real solutions.
There are no real solutions.
Solve for 
First isolate one of the radicals; the easiest would be the one with more than one term.
Square both sides of the equation,
Expand the right side,
Now collect terms and isolate the remaining radical expression; note the the 
Square both sides,
CHECK THE SOLUTION
We have done all of the algebra correctly, but we can still end up with an erroneous solution due to the squaring operation (a very similar problem arises when dealing with absolute value equations). Once you arrive at a solution, make sure you check that the solution works. If it does not work, and you know your algebra was right, then there are no real solutions.

Therefore there are no real solutions.
Example Question #474 : College Algebra
Solve for x:
no real solutions
using the quadratic formula we get
so the possible solutions are 



Example Question #53 : Solving Equations And Inequallities
Solve the radical equation:
Square both sides to eliminate the radical.
Divide by three on both sides to isolate the x.
The answer is:
Example Question #54 : Solving Equations And Inequallities
Solve the equation:
Square both sides.
Add 2 on both sides.
Divide by 3 on both sides.
The answer is:
Example Question #2 : Radical Equations
Which of the following are value(s) of 

First, isolate the radical on one side of the equation. Start by adding 
Now, square both sides of the equation.
Expand the right side of the equation.
Collect all the terms to one side of the equation and simplify to create a quadratic equation equal to zero.
Quadratic equations can be written in the following generic form:
We need to find two numbers whose product equals a multiplied by c and whose sum equals b; therefore, the product of the factors must be -12 and their sum must equal -1. Notice the following:
Write the two quantities. When c is negative, one quantity needs to have a plus sign and one needs to have a minus sign. When b is negative, the larger number should be associated with the minus sign. Write the following quadratic factorization:
The solutions for this quadratic are:
One common mistake for students is to assume that these solutions are—in fact—solutions to the original equation. Whenever you work with absolute value equations, or radical equations, you must check the solution carefully to make sure the solution actually works. As you will see, only one of the two solutions above actually works in this particular case.
We started with the following equation:
Now, substitute the solution 
We can see that -3 is not a solution. Now, substitute the solution 
The correct answer is 4.
Example Question #471 : College Algebra
Solve the following inequality.

To solve this inequality, we treat is a a regular equation. First, we add 8 to both sides.

We now divide both sides by 2 to get

Example Question #2 : Linear Inequalities
Solve:
To evaluate, we will need to multiply both sides by one-fifth.
The sign does not need to be switched unless we multiply or divide by a negative value.
The answer is:
Example Question #2 : Linear Inequalities
Express the following linear inequality in interval notation.
Upon solving for x, we find that x is larger than -2. The left-hand term of the interval is -2 since it is the lower bound for our set, and it has a parenthesis around it because it is not included in our set (-2 is not greater than -2). The right-hand term of the interval is positive infinity because any number larger than -2 is in the set. There is always a parenthesis around infinity or negative infinity.
Certified Tutor
Certified Tutor
All College Algebra Resources




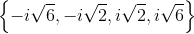









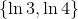










































































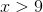

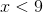
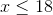










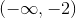

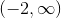

![\left [ -2,\infty \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1009903/gif.latex)



