All Calculus 3 Resources
Example Questions
Example Question #202 : Double Integrals
Find the surface area of the part of the plane 
Lets recall the equation of surface area.
Now we need to find all the neccessary equations to be able to evaluate the integral.
We will plug in 
Now we are going to set 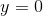
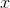
We now have all the bounds for our double integral
Example Question #3831 : Calculus 3
Evaluate 




First we need to evaluate the vector field evaluated along the curve.
Now we need to find the derivative of
Now we can do the product of 

Now we can put this into the integral and evaluate it.
Example Question #102 : Line Integrals
Find the work done by a particle moving in a force field 



The formula for work is given by

Writing our path in parametric equation form, we have

Hence
Plugging this into our work equation, we get

Example Question #1 : Line Integrals Of Vector Fields
Evaluate 



The line integral of a vector field is given by
So, we must evaluate the vector field on the curve:
Then, we take the derivative of the curve with respect to t:
Taking the dot product of these two vectors, we get
This is the integrand of our integral. Integrating, we get
Example Question #2 : Line Integrals Of Vector Fields
Evaluate the integral 


The line integral of the vector field is equal to
The parameterization (using the corresponding elements of the curve) of the vector field is
The derivative of the parametric curve is
Taking the dot product of the two vectors, we get
Integrating this with respect to t on the given interval, we get
Example Question #3 : Line Integrals Of Vector Fields
Calculate 


To calculate the line integral of the vector field, we must evaluate the vector field on the curve, take the derivative of the curve, and integrate the dot product on the given interval.
The vector field evaluated on the given curve is
The derivative of the curve is given by
The dot product of these is
Integrating this over our given t interval, we get
Example Question #1 : Surface Integrals
Let S be a known surface with a boundary curve, C.
Considering the integral 
In order to utilize Stokes' theorem, note its form
The curl of a vector function F over an oriented surface S is equivalent to the function F itself integrated over the boundary curve, C, of S.
Note that
From what we're told
Meaning that
From this we can derive our curl vectors
This allows us to set up our surface integral
Example Question #2 : Surface Integrals
Let S be a known surface with a boundary curve, C.
Considering the integral 
In order to utilize Stokes' theorem, note its form
The curl of a vector function F over an oriented surface S is equivalent to the function F itself integrated over the boundary curve, C, of S.
Note that
From what we're told
Meaning that
From this we can derive our curl vectors
This allows us to set up our surface integral
Example Question #3 : Surface Integrals
Let S be a known surface with a boundary curve, C.
Considering the integral 
In order to utilize Stokes' theorem, note its form
The curl of a vector function F over an oriented surface S is equivalent to the function F itself integrated over the boundary curve, C, of S.
Note that
From what we're told
Meaning that
From this we can derive our curl vectors
This allows us to set up our surface integral
Example Question #4 : Surface Integrals
Let S be a known surface with a boundary curve, C.
Considering the integral 
In order to utilize Stokes' theorem, note its form
The curl of a vector function F over an oriented surface S is equivalent to the function F itself integrated over the boundary curve, C, of S.
Note that
From what we're told
Meaning that
From this we can derive our curl vectors
This allows us to set up our surface integral
All Calculus 3 Resources

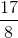




![S=\int \int_D \sqrt{[f_x]^2+[f_y]^2+1}\ dA](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/600202/gif.latex)


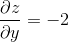


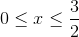

![S=\int_{0}^{\frac{3}{2}} \int_{0}^{\frac{3}{2}-x} \sqrt{[-2]^2+[-2]^2+1} \ dy \ dx](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/600215/gif.latex)

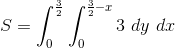


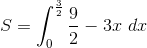































![\int \vec{F}\cdot d\vec{r} = \int [\vec{F}(\vec{r}(t))\cdot \vec{r'}(t)]dt](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/855983/gif.latex)









![\int_{0}^{1}[\vec{F}(\vec{r}(t))\cdot \vec{r'}(t)]dt](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/875547/gif.latex)














![\iint_{S}curl(\overrightarrow{F})\cdot d\overrightarrow{A} =[(12y^3z^3)\widehat{i}+(-9y^2z^4)\widehat{j}]\cdot\overrightarrow{A}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/679006/gif.latex)
![\iint_{S}curl(\overrightarrow{F})\cdot d\overrightarrow{A} =[(4y^3z^3)\widehat{j}+(-3y^2z^4)\widehat{k}]\cdot\overrightarrow{A}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/679002/gif.latex)
![\iint_{S}curl(\overrightarrow{F})\cdot d\overrightarrow{A} =[(4y^3z^3)\widehat{j}+(3y^2z^4)\widehat{k}]\cdot\overrightarrow{A}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/679003/gif.latex)
![\iint_{S}curl(\overrightarrow{F})\cdot d\overrightarrow{A} =[(12y^3z^3)\widehat{j}+(9y^2z^4)\widehat{k}]\cdot\overrightarrow{A}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/679005/gif.latex)
![\iint_{S}curl(\overrightarrow{F})\cdot d\overrightarrow{A} =[(12y^3z^3)\widehat{j}+(-9y^2z^4)\widehat{k}]\cdot\overrightarrow{A}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/679004/gif.latex)





![\iint_{S}curl(\overrightarrow{F})\cdot d\overrightarrow{A} =[(4y^3z^3)\widehat{j}+(-3y^2z^4)\widehat{k}]\cdot\overrightarrow{A}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/679091/gif.latex)

![\iint_{S}curl(\overrightarrow{F})\cdot d\overrightarrow{A} =[(x^2)\widehat{i}+(-2xy)\widehat{j}+(xcos{(xy)})\widehat{k}]\cdot\overrightarrow{A}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/679001/gif.latex)
![\iint_{S}curl(\overrightarrow{F})\cdot d\overrightarrow{A} =[(4x^2)\widehat{i}+(-2xy)\widehat{j}+(-xcos{(xy)})\widehat{k}]\cdot\overrightarrow{A}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/678998/gif.latex)
![\iint_{S}curl(\overrightarrow{F})\cdot d\overrightarrow{A} =[(x^2)\widehat{i}+(-2xy)\widehat{j}+(-xcos{(xy)})\widehat{k}]\cdot\overrightarrow{A}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/678997/gif.latex)
![\iint_{S}curl(\overrightarrow{F})\cdot d\overrightarrow{A} =[(x^2)\widehat{i}+(2xy)\widehat{j}+(-xcos{(xy)})\widehat{k}]\cdot\overrightarrow{A}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/679000/gif.latex)
![\iint_{S}curl(\overrightarrow{F})\cdot d\overrightarrow{A} =[(x^2)\widehat{i}+(2xy)\widehat{j}+(xcos{(xy)})\widehat{k}]\cdot\overrightarrow{A}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/678999/gif.latex)



![\iint_{S}curl(\overrightarrow{F})\cdot d\overrightarrow{A} =[(x^2)\widehat{i}+(-2xy)\widehat{j}+(-xcos{(xy)})\widehat{k}]\cdot\overrightarrow{A}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/679012/gif.latex)

![\iint_{S}curl(\overrightarrow{F})\cdot d\overrightarrow{A} =[(-z)\widehat{k}+(ycos{(xy)} - xe^{(xy)})\widehat{i}]\cdot\overrightarrow{A}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/678975/gif.latex)
![\iint_{S}curl(\overrightarrow{F})\cdot d\overrightarrow{A} =[(z)\widehat{i}+(ycos{(xy)} - xe^{(xy)})\widehat{k}]\cdot\overrightarrow{A}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/678972/gif.latex)
![\iint_{S}curl(\overrightarrow{F})\cdot d\overrightarrow{A} =[(z)\widehat{j}+(ycos{(xy)} - xe^{(xy)})\widehat{k}]\cdot\overrightarrow{A}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/678973/gif.latex)
![\iint_{S}curl(\overrightarrow{F})\cdot d\overrightarrow{A} =[(z)\widehat{i}+(ycos{(xy)}+xe^{(xy)})\widehat{j}]\cdot\overrightarrow{A}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/678974/gif.latex)
![\iint_{S}curl(\overrightarrow{F})\cdot d\overrightarrow{A} =[(x)\widehat{i}+(ycos{(xy)} - ye^{(xy)})\widehat{k}]\cdot\overrightarrow{A}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/678976/gif.latex)




![\iint_{S}curl(\overrightarrow{F})\cdot d\overrightarrow{A} =[(z)\widehat{i}+(ycos{(xy)} - xe^{(xy)})\widehat{k}]\cdot\overrightarrow{A}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/679029/gif.latex)
![\iint_{S}curl(\overrightarrow{F})\cdot d\overrightarrow{A} =[(-4cos{(4x)} + cos{(y)})\widehat{k}]\cdot\overrightarrow{A}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/679033/gif.latex)
![\iint_{S}curl(\overrightarrow{F})\cdot d\overrightarrow{A} =[(-4cos{(4x)} - cos{(y)})\widehat{k}]\cdot\overrightarrow{A}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/679032/gif.latex)
![\iint_{S}curl(\overrightarrow{F})\cdot d\overrightarrow{A} =[(4cos{(4x)} - cos{(y)})\widehat{k}]\cdot\overrightarrow{A}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/679030/gif.latex)
![\iint_{S}curl(\overrightarrow{F})\cdot d\overrightarrow{A} =[(4cos{(4x)} - cos{(y)})\widehat{j}]\cdot\overrightarrow{A}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/679034/gif.latex)
![\iint_{S}curl(\overrightarrow{F})\cdot d\overrightarrow{A} =[(4cos{(4x)} +cos{(y)})\widehat{k}]\cdot\overrightarrow{A}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/679031/gif.latex)



![\iint_{S}curl(\overrightarrow{F})\cdot d\overrightarrow{A} =[(4cos{(4x)} - cos{(y)})\widehat{k}]\cdot\overrightarrow{A}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/679065/gif.latex)



