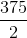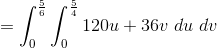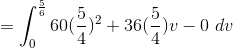All Calculus 3 Resources
Example Questions
Example Question #5 : Relative Minimums And Maximums
Find the relative maxima and minima of 






To find the relative maxima and minima, we must find all the first order and second order partial derivatives. We will use the first order partial derivative to find the critical points, then use the equation
to classify the critical points.
If 

If 

If 
If 
The first order partial derivatives are
The second order partial derivatives are
To find the critical points, we will set the first derivatives equal to
There is only one real value of 
We find the corresponding value of 

There is a critical point at 


At 
Since 

Example Question #6 : Relative Minimums And Maximums
Find the relative maxima and minima of 










To find the relative maxima and minima, we must find all the first order and second order partial derivatives. We will use the first order partial derivative to find the critical points, then use the equation
to classify the critical points.
If 

If 

If 
If 
The first order partial derivatives are
The second order partial derivatives are
To find the critical points, we will set the first derivatives equal to
The real values of 

We find the corresponding value of 

There are critical points at 



At 
Since 

At 
Since 

Example Question #3 : Relative Minimums And Maximums
Find the relative maxima and minima of 















To find the relative maxima and minima, we must find all the first order and second order partial derivatives. We will use the first order partial derivative to find the critical points, then use the equation
to classify the critical points.
If 

If 

If 
If 
The first order partial derivatives are
The second order partial derivatives are
To find the critical points, we will set the first derivatives equal to
Setting each factor in the expression equal to 

The real values of 


We find the corresponding value of 

There are critical points at 




At 
Since 

At 
Since 


At 
Since 


Example Question #8 : Relative Minimums And Maximums
Find the relative maxima and minima of 







To find the relative maxima and minima, we must find all the first order and second order partial derivatives. We will use the first order partial derivative to find the critical points, then use the equation
to classify the critical points.
If 

If 

If 
If 
The first order partial derivatives are
The second order partial derivatives are
To find the critical points, we will set the first derivatives equal to
Using a TI-83 or other software to find the root, we find that 
We find the corresponding value of 

There is a critical points at 


At 
Since 

Example Question #9 : Relative Minimums And Maximums
Find the relative maxima and minima of 
















































































To find the relative maxima and minima, we must find all the first order and second order partial derivatives. We will use the first order partial derivative to find the critical points, then use the equation
to classify the critical points.
If 

If 

If 
If 
The first order partial derivatives are
The second order partial derivatives are
To find the critical points, we will set the first derivatives equal to
Our derivatives equal 














We need to determine if the critical point is a maximum or minimum using 




Saddle point
minimum
minimum
Saddle point



maximum
saddle point
saddle point
maximum



maximum
saddle point
saddle point
maximum



saddle point
minimum
minimum
saddle point
Example Question #10 : Relative Minimums And Maximums
Find the relative maxima and minima of 





To find the relative maxima and minima, we must find all the first order and second order partial derivatives. We will use the first order partial derivative to find the critical points, then use the equation
to classify the critical points.
If 

If 

If 
If 
The first order partial derivatives are
The second order partial derivatives are
To find the critical points, we will set the first derivatives equal to
There is a critical point at 


At 
Since 


Example Question #11 : Relative Minimums And Maximums
Find the relative maxima and minima of 










To find the relative maxima and minima, we must find all the first order and second order partial derivatives. We will use the first order partial derivative to find the critical points, then use the equation
to classify the critical points.
If 

If 

If 
If 
The first order partial derivatives are
The second order partial derivatives are
To find the critical points, we will set the first derivatives equal to
The critical points are 



At 
Since 

At 
Since 

Example Question #12 : Relative Minimums And Maximums
Find the relative maxima and minima of 





To find the relative maxima and minima, we must find all the first order and second order partial derivatives. We will use the first order partial derivative to find the critical points, then use the equation
to classify the critical points.
If 

If 

If 
If 
The first order partial derivatives are
The second order partial derivatives are
To find the critical points, we will set the first derivatives equal to
The exponential part of each expression cannot equal 





The critical points are 



At 
Since 

Example Question #13 : Relative Minimums And Maximums
Find the relative maxima and minima of 





To find the relative maxima and minima, we must find all the first order and second order partial derivatives. We will use the first order partial derivative to find the critical points, then use the equation
to classify the critical points.
If 

If 

If 
If 
The first order partial derivatives are
The second order partial derivatives are
To find the critical points, we will set the first derivatives equal to
The exponential part of each expression cannot equal 





The critical point is 


At 
Since 

Example Question #681 : Multiple Integration
Evaluate 



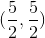

using the transformation 
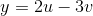
The first thing we have to do is figure out the general equations for the lines that create the trapezoid.
Now we have the general equations for out trapezoid, now we need to plug in our transformations into these equations.
So our region is a rectangle given by 
Next we need to calculate the Jacobian.
Now we can put the integral together.
Certified Tutor
Certified Tutor
All Calculus 3 Resources



















































![x=\sqrt[8]{-3*\frac{27}{-257}}=\pm \sqrt3/2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/788468/gif.latex)



























![\frac{\partial }{\partial x} \left (\frac{\partial f }{\partial x} \right )=f_{xx}(x,y)=2\left [ sin(x)(-sin(x))+cos(x)cos(x)\right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/788891/gif.latex)
![f_{xx}(x,y)=2\left [ -sin^2(x)+cos^2(x)\right ]=2cos^2(x)-2sin^2(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/788892/gif.latex)
![\frac{\partial }{\partial y} \left (\frac{\partial f }{\partial y} \right )=f_{yy}(x,y)=-2\left [ sin(y)(-sin(y))+cos(y)cos(y)\right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/788893/gif.latex)
![f_{yy}(x,y)=-2\left [ -sin^2(y)+cos^2(y)\right ]=2sin^2(y)-2cos^2(y)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/788894/gif.latex)















































































































^2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/789632/gif.latex)