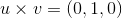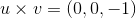This question can be solved with a simple u- substitution; 

Plugging in u and dx in our original integral gets us: 

Isolating  on the outside, as it is a constant, gets us: 

The integration of cos(u) is sin(u)+C:

Substitute back  gets us: 

This problem can be solved using a u-substitution: 

Plugging in u and dx gets us: 

The cos(x) factors cross out and simplifying get us: 

The integration of  is : 

Plugging in u = sin(x) from earlier get us our final answer: 

This problem can be solved using u-substitution, but instead of crossing out terms, we are manipulating the terms: 

Plugging in u and du into the original integral gets us: 

Since we cant cross out any terms, we will substitute  in terms of u by solving for x: 

Now that we found our  term in terms of u, we can substitute it in our equation above: 

We can now expand and simplify from there: 

Then we can integrate from there: 

Substituting u = x-1 from earlier gets us:

We notice that the powers of the functions within the numerator and denominator are the same, which means we need to rewrite the function: 

We first isolate the any constants to make the problem easier: 

We then rewrite the function  into  though long division or any other method: 

Now we integrate each term: 

To find, , we apply u-substitution: 

Plugging in u and du, we get: 

The integral of  is , and we get: 

Substituting u = x-4 from earlier, we get our final answer: 

At first glance, we notice that the tangent power is odd and positive. Since it is odd, we then save a secant-tangent factor and convert the remaining factors to secants: 

Ignoring the secant- tangent factor, convert the remaining factors to secant functions: 

Using the trig identity, , convert 

Now, we are free to use u- substitution at this point: 

Substituting u and dx for the above equation, we now get: 

We can then cross out the sec(x)tan(x) factor to now get: 

Expand and simplify factors: 

Using the basic formula , we can now integrate the function: 

Now substitute the remaining u's with u = sec(x): 

Simplifying, we get: 

This question looks extremely difficult without thinking at first, but it is simple problem by breaking it into separate integrals: 

We then apply u substitution to each of the two separate integrals. starting with : 

Plugging in for u and dx get us: 

Isolate constants: 

The integration of  is : 

Plugging in , we now get: 

For the second integral, , we also apply u substitution, but using a different variable to avoid confusion: 

Plugging y and dy into the integral gets us: 

, 

which equals: 

Plugging in y = x+1, we now get: 

Combining two results together gets us our final result: 

We are trying to find the cross product between  and .

Recall the formula for cross product.

If  , and , then

.

Now apply this to our situation.

We are trying to find the cross product between  and .

Recall the formula for cross product.

If  , and , then

.

Now apply this to our situation.

This is true. The cross product is defined this way. The dot product however can be taken for two vectors of dimension n (provided that both vectors are the same dimension).

By definition, the order of the dot product of two vectors does not matter, as the final output is a scalar.  However, the cross product of two vectors will change signs depending on the order that they are crossed.  Therefore 

.