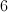Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : Integrals

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #41 : Integrals

Solve the separable differential equation

$\frac{\mathrm{d} y}{\mathrm{d} x} = y(2x+x^2)$ $\displaystyle \frac{\mathrm{d} y}{\mathrm{d} x} = y(2x+x^2)$

given the initial condition

f(0)=14 $\displaystyle f(0)=14$

Possible Answers:

$y=14e^{2x+\frac{x^3}{3}}$ $\displaystyle y=14e^{2x+\frac{x^3}{3}}$

$y=Ce^{x^2+\frac{x^3}{3}}$ $\displaystyle y=Ce^{x^2+\frac{x^3}{3}}$

$y=14e^{x^2+\frac{x^3}{3}}$ $\displaystyle y=14e^{x^2+\frac{x^3}{3}}$

$y=14e^{\frac{x^2}{2}+\frac{x^3}{3}}$ $\displaystyle y=14e^{\frac{x^2}{2}+\frac{x^3}{3}}$

$y=14e^{x^2+\frac{x^2}{3}}$ $\displaystyle y=14e^{x^2+\frac{x^2}{3}}$

Correct answer:

$y=14e^{x^2+\frac{x^3}{3}}$ $\displaystyle y=14e^{x^2+\frac{x^3}{3}}$

Explanation:

To solve the separable differential equation, we must separate x and y to the same sides as their respective derivatives:

$\frac{dy}{y} = (2x+x^2)dx$ $\displaystyle \frac{dy}{y} = (2x+x^2)dx$

Next, we integrate both sides:

$\ln \left | y\right |= x^2+\frac{x^3}{3}+C$ $\displaystyle \ln \left | y\right |= x^2+\frac{x^3}{3}+C$

The integrals were solved using the following rules:

$\int \frac{dx}{x}=\ln \left | x\right |+C$ $\displaystyle \int \frac{dx}{x}=\ln \left | x\right |+C$, $\int x^n dx = \frac{x^{n+1}}{n+1}+C$ $\displaystyle \int x^n dx = \frac{x^{n+1}}{n+1}+C$

The two constants of integration were combined to make a single constant.

Now, exponentiate both sides to isolate y, and use the properties of exponents to rearrange the integration constant:

$e^{\ln\left | y\right |}= e^{x^2+\frac{x^3}{3}+C}$ $\displaystyle e^{\ln\left | y\right |}= e^{x^2+\frac{x^3}{3}+C}$

$y=e^{x^2+\frac{x^3}{3}}\cdot e^C=Ce^{x^2+\frac{x^3}{3}}$ $\displaystyle y=e^{x^2+\frac{x^3}{3}}\cdot e^C=Ce^{x^2+\frac{x^3}{3}}$

(The exponential of the constant is another constant.)

Finally, we solve for the integration constant using the initial condition:

$\displaystyle 14=Ce^0=C$

Our final answer is

$y=14e^{x^2+\frac{x^3}{3}}$ $\displaystyle y=14e^{x^2+\frac{x^3}{3}}$

Report an Error

Example Question #42 : Integrals

Solve the separable differential equation:

$\frac{\mathrm{d} y}{\mathrm{d} x} = \frac{x^4+e^x}{2y}, y< 0$ $\displaystyle \frac{\mathrm{d} y}{\mathrm{d} x} = \frac{x^4+e^x}{2y}, y< 0$

Possible Answers:

$y=\sqrt{\frac{x^5}{5}+e^x+C}$ $\displaystyle y=\sqrt{\frac{x^5}{5}+e^x+C}$

$y=\sqrt{\frac{x^5}{5}+e^x}+C$ $\displaystyle y=\sqrt{\frac{x^5}{5}+e^x}+C$

$y=-\sqrt{\frac{x^5}{5}+e^x+C}$ $\displaystyle y=-\sqrt{\frac{x^5}{5}+e^x+C}$

$y=-\sqrt{{x^5}+e^x+C}$ $\displaystyle y=-\sqrt{{x^5}+e^x+C}$

Correct answer:

$y=-\sqrt{\frac{x^5}{5}+e^x+C}$ $\displaystyle y=-\sqrt{\frac{x^5}{5}+e^x+C}$

Explanation:

To solve the separable differential equation, we must separate x and y to the same sides as their respective derivatives:

$\displaystyle 2y dy=(x^4+x)dx$

Next, we integrate both sides:

$y^2=\frac{x^5}{5}+e^x+C$ $\displaystyle y^2=\frac{x^5}{5}+e^x+C$

The integrals were solved using the following rules:

$\int x^ndx=\frac{x^{n+1}}{n+1}+C$ $\displaystyle \int x^ndx=\frac{x^{n+1}}{n+1}+C$, $\int e^x dx=e^x+C$ $\displaystyle \int e^x dx=e^x+C$

The two constants of integration were combined to make a single one.

Now, we solve for y:

$y=\pm \sqrt{\frac{x^5}{5}+e^x+C}$ $\displaystyle y=\pm \sqrt{\frac{x^5}{5}+e^x+C}$

Because the problem statement said that y is negative - and y cannot be zero - our final answer is

$y=-\sqrt{\frac{x^5}{5}+e^x+C}$ $\displaystyle y=-\sqrt{\frac{x^5}{5}+e^x+C}$

Report an Error

Example Question #43 : Integrals

Solve the separable differential equation:

$\frac{\mathrm{d} y}{\mathrm{d} x} = \frac{4y}{x^2}, x>0$ $\displaystyle \frac{\mathrm{d} y}{\mathrm{d} x} = \frac{4y}{x^2}, x>0$

and at $\displaystyle x=1, y=2$

Possible Answers:

$y=Ce^{-\frac{4}{x}}$ $\displaystyle y=Ce^{-\frac{4}{x}}$

$y=2e^{-\frac{4}{x}}$ $\displaystyle y=2e^{-\frac{4}{x}}$

$y=2e^{-\frac{4}{x}}+C$ $\displaystyle y=2e^{-\frac{4}{x}}+C$

$y=2e^{4-\frac{4}{x}}$ $\displaystyle y=2e^{4-\frac{4}{x}}$

y=2 $\displaystyle y=2$

Correct answer:

$y=2e^{4-\frac{4}{x}}$ $\displaystyle y=2e^{4-\frac{4}{x}}$

Explanation:

To solve the separable differential equation, we must separate x and y to the same sides as their respective derivatives:

$\frac{dy}{y}=\frac{dx}{x^2}$ $\displaystyle \frac{dy}{y}=\frac{dx}{x^2}$

Next, we integrate both sides:

$\ln \left | y\right | = -\frac{1}{x}+C$ $\displaystyle \ln \left | y\right | = -\frac{1}{x}+C$

The integrals were solved using the following rules:

$\int \frac{dx}{x}= \ln \left | x\right |+C$ $\displaystyle \int \frac{dx}{x}= \ln \left | x\right |+C$, $\int x^n dx = \frac{x^{n+1}}{n+1}+C$ $\displaystyle \int x^n dx = \frac{x^{n+1}}{n+1}+C$

The two constants of integration were combined to make a single one.

Now, we exponentiate both sides to solve for y:

$y=e^{-\frac{1}{x}+C}$ $\displaystyle y=e^{-\frac{1}{x}+C}$

Using the properties of exponents, we can rearrange the integration constant:

$y=e^{-\frac{1}{x}+C} = e^{-\frac{1}{x}}\cdot e^C = Ce^{-\frac{1}{x}}$ $\displaystyle y=e^{-\frac{1}{x}+C} = e^{-\frac{1}{x}}\cdot e^C = Ce^{-\frac{1}{x}}$

(The exponential of the constant is itself a constant.)

Using the given condition, we can solve for C:

$2=Ce^{-4}$ $\displaystyle 2=Ce^{-4}$

C=2e^4 $\displaystyle C=2e^4$

Our final answer is

$y=2e^{4-\frac{4}{x}}$ $\displaystyle y=2e^{4-\frac{4}{x}}$

Report an Error

Example Question #44 : Integrals

The rate of a chemical reaction is given by the following differential equation:

$\frac{-d[A]}{dt} = k[A]^{2}$ $\displaystyle \frac{-d[A]}{dt} = k[A]^{2}$,

where $\left [ A \right ]$ $\displaystyle \left [ A \right ]$ is the concentration of compound $\displaystyle A$ at a given time, $\displaystyle t$. Which one of the following equations describes $\frac{1}{\left [ A \right ]}$ $\displaystyle \frac{1}{\left [ A \right ]}$ as a function of time? Let $\left [ A \right ]_{0}$ $\displaystyle \left [ A \right ]_{0}$ be the concentration of compound $\displaystyle A$ when t=0 $\displaystyle t=0$.

Possible Answers:

$\frac{1}{[A_{0}]} + kt = \frac{1}{[A]}$ $\displaystyle \frac{1}{[A_{0}]} + kt = \frac{1}{[A]}$

$[A_{0}]kt= \frac{1}{[A]}$ $\displaystyle [A_{0}]kt= \frac{1}{[A]}$

$\frac{1}{[A_{0}]} - kt = \frac{1}{[A]}$ $\displaystyle \frac{1}{[A_{0}]} - kt = \frac{1}{[A]}$

$[A_{0}]e^{-kt}= \frac{1}{[A]}$ $\displaystyle [A_{0}]e^{-kt}= \frac{1}{[A]}$

$[A_{0}]e^{kt}= \frac{1}{[A]}$ $\displaystyle [A_{0}]e^{kt}= \frac{1}{[A]}$

Correct answer:

$\frac{1}{[A_{0}]} + kt = \frac{1}{[A]}$ $\displaystyle \frac{1}{[A_{0}]} + kt = \frac{1}{[A]}$

Explanation:

To begin with, the differential equation needs to be rearranged so that each variable is one side of the equation:

$\frac{-d[A]}{dt} = k[A]^{2} \Rightarrow \frac{d[A]}{[A]^{2}} = -kdt$ $\displaystyle \frac{-d[A]}{dt} = k[A]^{2} \Rightarrow \frac{d[A]}{[A]^{2}} = -kdt$.

Then, integrate each side of the rate law, bearing in mind that $\left [ A \right ]$ $\displaystyle \left [ A \right ]$ will range from $\left [ A \right ]_{0}$ $\displaystyle \left [ A \right ]_{0}$ to $\left [ A \right ]$ $\displaystyle \left [ A \right ]$, and time will range from $\displaystyle 0$ to $\displaystyle t$:

$\int_{[A]_{0}}^{[A]}\frac{d[A]}{[A]^{2}} = \int_{0}^{t} -kdt$ $\displaystyle \int_{[A]_{0}}^{[A]}\frac{d[A]}{[A]^{2}} = \int_{0}^{t} -kdt$

After integrating each side, the equation becomes:

$\frac{-1}{[A]} = -kt$ $\displaystyle \frac{-1}{[A]} = -kt$.

The left side has to be evaluated from $\left [ A \right ]_{0}$ $\displaystyle \left [ A \right ]_{0}$ to $\left [ A \right ]$ $\displaystyle \left [ A \right ]$, and the right side is evaluated from $\displaystyle 0$ to $\displaystyle t$:

$\frac{-1}{[A]} - ( \frac{-1}{[A_{0}]}) = -kt - (-k(0))$ $\displaystyle \frac{-1}{[A]} - ( \frac{-1}{[A_{0}]}) = -kt - (-k(0))$. This becomes:

$\frac{1}{[A_{0}]} - \frac{1}{[A]} = -kt$ $\displaystyle \frac{1}{[A_{0}]} - \frac{1}{[A]} = -kt$.

Finally, rearranging gives:

$\frac{1}{[A_{0}]} + kt = \frac{1}{[A]}$ $\displaystyle \frac{1}{[A_{0}]} + kt = \frac{1}{[A]}$

Report an Error

Example Question #45 : Integrals

Given that $\displaystyle y' = (2y + 2)(x -2)$ and $\displaystyle y(0) = 1$, solve for y(t) $\displaystyle y(t)$. What is the value of $\displaystyle y(4)$?

Possible Answers:

2e - 1 $\displaystyle 2e - 1$

$\displaystyle -1$

$\displaystyle 64$

$\displaystyle 2e^2 - 1$

Correct answer:

Explanation:

This is a separable differential equation. The simplest way to approach this is to turn $\displaystyle y'$ into $\frac{\mathrm{d} y}{\mathrm{d} x}$ $\displaystyle \frac{\mathrm{d} y}{\mathrm{d} x}$, and then by abusing the notation, "multiplying by dx" on both sides.

$\displaystyle dy = (2y+2)(x - 2)dx$

We then group all the y terms with dy, and all the x terms with dx.

$\frac{1}{2y+2}dy = (x - 2)dx$ $\displaystyle \frac{1}{2y+2}dy = (x - 2)dx$

Integrating both sides, we find

$\int \frac{1}{2y+2}dy = \frac{\ln|2y+2|}{2} =\int (x - 2)dx = \frac{x^2}{2} - 2x + C$ $\displaystyle \int \frac{1}{2y+2}dy = \frac{\ln|2y+2|}{2} =\int (x - 2)dx = \frac{x^2}{2} - 2x + C$

Here, the first integral is found by using substitution of variables, setting $\displaystyle u = 2y +2$. In addition, we have chosen to only put a +C on the second integral, as if we put it on both, we would just combine them in any case.

To solve for y, we multiply both sides by two and raise e to both sides to get rid of the natural logarithm.

$|2y+2| = e^{x^2 - 4x + C}$ $\displaystyle |2y+2| = e^{x^2 - 4x + C}$

(Note, C was multiplied by two, but it's still just an arbitrary constant. If you prefer, you may call the new C value C_1 $\displaystyle C_1$.)

Now we drop our absolute value signs, and note that we can take out a factor of e^C $\displaystyle e^C$ and stick in front of the right hand side.

$2y+2 =\pm e^Ce^{x^2 - 4x}$ $\displaystyle 2y+2 =\pm e^Ce^{x^2 - 4x}$

As $\pm e^C$ $\displaystyle \pm e^C$ is just another arbitrary constant, we can relabel this as C, or C_2 $\displaystyle C_2$ if you prefer. Solving for y gets us

$y = \frac{Ce^{x^2 - 4x} - 2}{2}$ $\displaystyle y = \frac{Ce^{x^2 - 4x} - 2}{2}$

Next, we plug in our initial condition to solve for C.

$1 =\frac{C - 2}{2}$ $\displaystyle 1 =\frac{C - 2}{2}$; C = 4 $\displaystyle C = 4$

Leaving us with a final equation of

$y = \frac{4e^{x^2 - 4x} - 2}{2}$ $\displaystyle y = \frac{4e^{x^2 - 4x} - 2}{2}$

Plugging in x = 4, we have a final answer,

$y = \frac{4e^{16 - 16} - 2}{2} = \frac{4 - 2}{2} = 1$ $\displaystyle y = \frac{4e^{16 - 16} - 2}{2} = \frac{4 - 2}{2} = 1$

Report an Error

Example Question #46 : Integrals

Solve the separable differential equation:

$\frac{\mathrm{d} y}{\mathrm{d} x}=y\cos(x)$ $\displaystyle \frac{\mathrm{d} y}{\mathrm{d} x}=y\cos(x)$

given the condition at

$x=\pi, y=2$ $\displaystyle x=\pi, y=2$

Possible Answers:

y=x $\displaystyle y=x$

$y=Ce^{\sin(x)}$ $\displaystyle y=Ce^{\sin(x)}$

$y=e^{\sin(x)}$ $\displaystyle y=e^{\sin(x)}$

$y=2e^{\sin(x)}$ $\displaystyle y=2e^{\sin(x)}$

Correct answer:

$y=2e^{\sin(x)}$ $\displaystyle y=2e^{\sin(x)}$

Explanation:

To solve the separable differential equation, we must separate x and y to the same sides as their respective derivatives:

$\frac{dy}{y}=\cos(x)dx$ $\displaystyle \frac{dy}{y}=\cos(x)dx$

Next, we integrate both sides:

$\int \frac{dy}{y}=\ln\left | y\right |+C$ $\displaystyle \int \frac{dy}{y}=\ln\left | y\right |+C$; $\int \cos(x)dx=\sin(x)+C$ $\displaystyle \int \cos(x)dx=\sin(x)+C$

The integrals were solved using the identical rules.

The two constants of integration are now combined to make a single one:

$\ln \left | y\right |= \sin(x)+C$ $\displaystyle \ln \left | y\right |= \sin(x)+C$

Now, exponentiate both sides of the equation to solve for y, and use the properties of exponents to rearrange C:

$y=e^{\sin(x)+C}=e^{\sin(x)}\cdot e^C=Ce^{\sin(x)}$ $\displaystyle y=e^{\sin(x)+C}=e^{\sin(x)}\cdot e^C=Ce^{\sin(x)}$

Finally, we solve for the integration constant using the given condition:

$2=Ce^{\sin(\pi)}=Ce^0=C$ $\displaystyle 2=Ce^{\sin(\pi)}=Ce^0=C$

Our final answer is

$y=2e^{\sin(x)}$ $\displaystyle y=2e^{\sin(x)}$

Report an Error

Example Question #47 : Integrals

If f(1) = 12, f' is continuous, and the integral from 1 to 4 of f'(x)dx = 16, what is the value of f(4)?

Possible Answers:

Correct answer:

Explanation:

You are provided f(1) and are told to find the value of f(4). By the FTC, the following follows:

(integral from 1 to 4 of f'(x)dx) + f(1) = f(4)

16 + 12 = 28

Report an Error

Example Question #1 : Interpretations And Properties Of Definite Integrals

Find the limit.

lim as n approaches infiniti of ((4n³) – 6n)/((n³) – 2n²+ 6)

Possible Answers:

nonexistent

–6

Correct answer:

Explanation:

lim as n approaches infiniti of ((4n³) – 6n)/((n³) – 2n²+ 6)

Use L'Hopitals rule to find the limit.

lim as n approaches infiniti of ((4n³) – 6n)/((n³) – 2n²+ 6)

lim as n approaches infiniti of ((12n²) – 6)/((3n²) – 4n + 6)

lim as n approaches infiniti of 24n/(6n – 4)

lim as n approaches infiniti of 24/6

The limit approaches 4.

Report an Error

Example Question #2 : Definite Integral Of The Rate Of Change Of A Quantity Over An Interval Interpreted As The Change Of The Quantity Over The Interval

If a particle's movement is represented by $p=3t^{2}-t+16$ $\displaystyle p=3t^{2}-t+16$, then when is the velocity equal to zero?

Possible Answers:

$\displaystyle 1$

$\frac{1}{6}$ $\displaystyle \frac{1}{6}$

$\displaystyle 16$

$\displaystyle 0$

$\displaystyle 6$

Correct answer:

$\frac{1}{6}$ $\displaystyle \frac{1}{6}$

Explanation:

The answer is $\frac{1}{6}$ $\displaystyle \frac{1}{6}$ seconds.

$p=3t^{2}-t+16$ $\displaystyle p=3t^{2}-t+16$

$v=p'=6t-1$ $\displaystyle v=p'=6t-1$

now set v=0 $\displaystyle v=0$ because that is what the question is asking for.

$v=0=6t-1$ $\displaystyle v=0=6t-1$

$t=\frac{1}{6}$ $\displaystyle t=\frac{1}{6}$ seconds

Report an Error

Example Question #3 : Definite Integral Of The Rate Of Change Of A Quantity Over An Interval Interpreted As The Change Of The Quantity Over The Interval

A particle's movement is represented by $p=-t^{2}+12t+2$ $\displaystyle p=-t^{2}+12t+2$

At what time is the velocity at it's greatest?

Possible Answers:

$\displaystyle 12$

$\displaystyle -2$

$\displaystyle 6$

$\displaystyle 0$

$\displaystyle 2$

Correct answer:

$\displaystyle 6$

Explanation:

The answer is at 6 seconds.

$p=-t^{2}+12t+2$ $\displaystyle p=-t^{2}+12t+2$

We can see that this equation will look like a upside down parabola so we know there will be only one maximum.

$v=p'=-2t+12$ $\displaystyle v=p'=-2t+12$

Now we set v=0 $\displaystyle v=0$ to find the local maximum.

$v=0=-2t+12$ $\displaystyle v=0=-2t+12$

$t=6$ $\displaystyle t=6$ seconds

Report an Error

View AP Calculus AB Tutors

Harriet
Certified Tutor

St. Olaf College, Bachelors, Math and Physics.

View AP Calculus AB Tutors

Evgenii
Certified Tutor

View AP Calculus AB Tutors

Steven
Certified Tutor

Florida International University, Bachelor of Science, Biology, General.

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Algebra Tutors in Phoenix, SAT Tutors in New York City, Physics Tutors in Denver, Computer Science Tutors in Houston, GRE Tutors in Atlanta, French Tutors in Denver, Computer Science Tutors in Chicago, Chemistry Tutors in Seattle, Algebra Tutors in Atlanta, Calculus Tutors in San Francisco-Bay Area

Popular Courses & Classes

ISEE Courses & Classes in Phoenix, GRE Courses & Classes in Phoenix, SAT Courses & Classes in Chicago, Spanish Courses & Classes in Washington DC, SAT Courses & Classes in Houston, ISEE Courses & Classes in Los Angeles, ISEE Courses & Classes in Miami, ACT Courses & Classes in Washington DC, ISEE Courses & Classes in Philadelphia, Spanish Courses & Classes in San Diego

Popular Test Prep

ISEE Test Prep in Houston, GRE Test Prep in Seattle, LSAT Test Prep in Atlanta, ACT Test Prep in Washington DC, GRE Test Prep in San Diego, GMAT Test Prep in Dallas Fort Worth, SAT Test Prep in New York City, GMAT Test Prep in Denver, GRE Test Prep in Miami, SAT Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : Integrals

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #41 : Integrals

Example Question #42 : Integrals

Example Question #43 : Integrals

Example Question #44 : Integrals

Example Question #45 : Integrals

Example Question #46 : Integrals

Example Question #47 : Integrals

Example Question #1 : Interpretations And Properties Of Definite Integrals

Example Question #2 : Definite Integral Of The Rate Of Change Of A Quantity Over An Interval Interpreted As The Change Of The Quantity Over The Interval

Example Question #3 : Definite Integral Of The Rate Of Change Of A Quantity Over An Interval Interpreted As The Change Of The Quantity Over The Interval

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: