All AP Calculus AB Resources
Example Questions
Example Question #1 : Definite Integral As A Limit Of Riemann Sums
True or False: If 


False
True
True
This is true. Since 



Example Question #2 : Definite Integral As A Limit Of Riemann Sums

![\left [ 1,10 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/88137/gif.latex)






![\left [ 1,10 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/37506/gif.latex)




![\left [ 1,10 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/37508/gif.latex)

![\left [ 1,10 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/37504/gif.latex)



According to Rolle's Theorem, if a function is continuous over a closed interval ![\left [ a,b \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/118401/gif.latex)





Example Question #3 : Definite Integral As A Limit Of Riemann Sums
You may use one or both of the following summation formulas:
Express the following definite integral as a limit of Riemman Sums. Then evaluate the integral by evaluating the limit.
First, let's remind ourselves what the formula for Riemann Sums is. Written in Summation form, it is:
when 
To use this formula, we need to do three things:
(1) we need to find
(2) we need to develop a formula for
(3) we need to plug that 
To find 






Plugging in 

Now we have 

First, we know that the left endpoint of the 1st subinterval is 

To get the 2nd right endpoint, we just add a 2nd 
to get the "i-th" right endpoint, we just add 
This is the "i-th" concept. Now if we wanted the 50th rigth endpoint, we would just plug 50 in for "i". Fortunately, we don't need to.
Now we have 



Plugging in to this function we get
Recall that we determined 
To simplify, we will combine the 1 and -1 to cancel them, and then apply the square power to what is left.
Now we have all the pieces of the Limit of Riemann sums formula. Let's plug them in.
To evaluate the limit, we must first find the sum. To do this, we must realize that we can pull any common factors out of the summation, as long as they are constant with respect to the summation index 


like this:
By passing the 
This means we can evaluate the sum by replacing it using the above formula.
Doing this, we get:
Now we can start evaluating the limit.
Lets start by reducing the single 

Now we will multiply our the two factors on top, and also multiply the 
Combining like terms, we get
Since the denominator is a single term, we can split the big fraction into three individual fractions, and reduce each one.
Remember that the limit of a constant is equal to that constant. Also remember when evaluating limits at infinity, a constant divided by a variable equals zero.
Applying these, we get
This gives us the correct answer of
Example Question #1 : Calculus I — Derivatives
Consider the function
Find the minimum of the function on the interval ![\left [ 0,1 \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/90588/gif.latex)
To find potential minima of the function, take the first derivative of 
Set the derivative to 0:
We solve for 

We can double check that 
which means the function is concave up, so that the point we found is a minimum.
Example Question #4 : Techniques Of Antidifferentiation
Find the x coordinate of the minimum of 
![\left [ -2, 2\right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/106125/gif.latex)
First, find the derivative, which is:
Set that equal to 0 to find your critical points:
Evaluate f at each critical point and endpoint over [-2, 2]:
The least of those numbers is the minimum. Because f(-2)=-32, that is the minimum.
Example Question #4 : Properties Of Graphs
What is the local minimum of 

There is no local minimum in that range.
The y-value is constant throughout that range.
To find the maximum, we need to look at the first derivative.
To find the first derivative, we can use the power rule. To do that, we lower the exponent on the variables by one and multiply by the original exponent.
We're going to treat 

Notice that 
When looking at the first derivative, remember that if the output of this equation is positive, the original function is increasing. If the derivative is negative, then the function is decreasing.
Because we want the MINIMUM, we want to see where the derivative changes from negative to positive.
Notice that 


Example Question #1 : Techniques Of Antidifferentiation
Integrate,


Integrate
1) Apply the sum rule for integration,
2) Integrate each individual term and include a constant of integration,
Further Discussion
Since indefinite integration is essentially a reverse process of differentiation, check your result by computing its' derivative.
This is the same function we integrated, which confirms our result. Also, because the derivative of a constant is always zero, we must include "C" in our result since any constant added to any function will produce the same derivative.
Example Question #5 : Techniques Of Antidifferentiation
Example Question #1 : Antiderivatives Following Directly From Derivatives Of Basic Functions
Example Question #2 : Antiderivatives Following Directly From Derivatives Of Basic Functions
Certified Tutor
Certified Tutor
All AP Calculus AB Resources
























![\lim_{n \to \infty} \sum_{i=1}^n [(\frac{i^2}{n^2})(\frac{1}{n})]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1062325/gif.latex)


![\lim_{n \to \infty} \frac{1}{n^3} [\frac{n(n+1)(2n+1)}{6}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1062332/gif.latex)
![\lim_{n \to \infty} \frac{1}{n^2} [\frac{(n+1)(2n+1)}{6}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1062335/gif.latex)








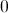
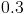
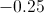






















![\int[x^2 +\sin(x)-3]dx](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/749356/gif.latex)




![\int[x^2 +\sin(x)-3]dx](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/749357/gif.latex)








![\begin{align*}&\text{In performing an integral, familiarity with derivative rules}\\&\text{can prove useful. After all, an integral is essentially the}\\&\text{opposite operation of a derivative. Consider how in a derivative}\\&\text{we’d use the chain rule to multiply the derivative of the “inside”}\\&\text{of a function by the derivative of the outside? Integrals, in}\\&\text{similar fashion, entail a division.}\\&\text{Utilizing integral rules:}\\&\int[cos(ax)]=\frac{sin(ax)}{a}\\&\int_{8}^{11.5}(\frac{(27cos(x + 1))}{8})dx=\frac{(27sin(x + 1))}{8}|_{8}^{11.5}\\&\text{Now we just subtract the function value at the lower bound from that of the upper bound:}\\&\int_{8}^{11.5}(\frac{(27cos(x + 1))}{8})dx=\frac{(27sin((11.5) + 1))}{8}-(\frac{(27sin((8) + 1))}{8})\\&\int_{8}^{11.5}(\frac{(27cos(x + 1))}{8})dx=-1.61\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/931547/gif.latex)











![\begin{align*}&\text{In performing an integral, familiarity with derivative rules}\\&\text{can prove useful. After all, an integral is essentially the}\\&\text{opposite operation of a derivative. Consider how in a derivative}\\&\text{we’d use the chain rule to multiply the derivative of the “inside”}\\&\text{of a function by the derivative of the outside? Integrals, in}\\&\text{similar fashion, entail a division.}\\&\text{Utilizing integral rules:}\\&\int[b^{ax}]=\frac{b^{ax}}{aln(b)}\\&\int_{-6}^{-3}(\frac{(10\cdot 2^{(\frac{x}{4})})}{7})dx=\frac{(40\cdot 2^{(\frac{x}{4})})}{(7ln(2))}|_{-6}^{-3}\\&\text{Now we just subtract the function value at the lower bound from that of the upper bound:}\\&\int_{-6}^{-3}(\frac{(10\cdot 2^{(\frac{x}{4})})}{7})dx=\frac{(40\cdot 2^{(\frac{(-3)}{4})})}{(7ln(2))}-(\frac{(40\cdot 2^{(\frac{(-6)}{4})})}{(7ln(2))})\\&\int_{-6}^{-3}(\frac{(10\cdot 2^{(\frac{x}{4})})}{7})dx=1.99\end{align*}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/931641/gif.latex)



