Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #21 : Implicit Differentiation

Use implicit differentiation to calculate the equation of the line tangent to the equation $2x^{2}+y^{2}=9$ at the point (2,1).

Possible Answers:

y=4x+9

y=-4x-9

y=-4x+9

y=4x-9

Correct answer:

y=-4x+9

Explanation:

Differentiate both sides of the equation: $\frac{\mathrm{d} }{\mathrm{d} x}(2x^{2}+y^{2}=9)$

Simplify: $4x+\frac{\mathrm{d} }{\mathrm{d} x}y^{2}=0$

Use implicit differentiation to differentiate the y term: $4x+2y\frac{dy}{dx}=0$

Subtract 4x from both sides of the equation: $2y\frac{dy}{dx}=-4x$

Divide both sides of the equation by 2y: $\frac{dy}{dx}=\frac{-4x}{2y}=\frac{-2x}{y}$

Plug in the appropriate values for x and y to find the slope of the tangent line: $m=\frac{-2(2)}{(1)}=-4$

Use slope-intercept form to solve for the equation of the tangent line: y=mx+b=y=-4x+b

Plug in the appropriate values of x and y into the equation, to find the equation of the tangent line: 1=(2)(-4)+b

Solve for b: 1=-8+b

b=9

Solution: y=-4x+9

Report an Error

Example Question #21 : Implicit Differentiation

Find $\frac{\mathrm{d} z}{\mathrm{d} x}$ , where is a function of x.

Possible Answers:

$\frac{3-z}{x+2z}$

$\frac{3-2z}{x}$

$\frac{-z}{x+2z}$

Correct answer:

$\frac{3-z}{x+2z}$

Explanation:

To find $\frac{\mathrm{d} z}{\mathrm{d} x}$ we must use implicit differentiation, which is an application of the chain rule.
Taking $\frac{\mathrm{d} }{\mathrm{d} x}$ of both sides of the equation, we get

$z+x\frac{\mathrm{d} z}{\mathrm{d} x}+2z\frac{\mathrm{d} z}{\mathrm{d} x}=3$

and the derivatives were found using the following rules:

$\frac{\mathrm{d} }{\mathrm{d} x} f(g(x))=f'(g(x))\cdot g'(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} f(x)g(x)=f'(x)g(x)+f(x)g'(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} ax=a$ , $\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$
Note that for every derivative of a function with z, the additional term $\frac{\mathrm{d} z}{\mathrm{d} x}$ appears; this is because of the chain rule, where z=g(x), so to speak, for the function it appears in.

Using algebra to solve, we get

$\frac{\mathrm{d} z}{\mathrm{d} x}=\frac{3-z}{x+2z}$

Report an Error

Example Question #31 : Implicit Differentiation

Find the normal line of the curve $\frac{x^{2}}{2}+y^{2}=4$ at the point $(1,\frac{\sqrt{14}}{2})$

Possible Answers:

$y=x\sqrt{14}-\frac{\sqrt{14}}{2}$

$y=2x\sqrt{14}-\frac{\sqrt{14}}{2}$

$y=x\sqrt{14}-{\sqrt{14}}$

$y=x\sqrt{14}+\frac{\sqrt{14}}{2}$

Correct answer:

$y=x\sqrt{14}-\frac{\sqrt{14}}{2}$

Explanation:

$\frac{x^{2}}{2}+y^{2}=4$

Use implicit differentiation to calculate the slope of the tangent line:

$\frac{\mathrm{d} }{\mathrm{d} x}(\frac{x^{2}}{2}+y^{2}=4)$

$\frac{2x}{2}+2y\frac{dy}{dx}=0$

Simplify: $x+2y\frac{dy}{dx}=0$

Subtract x from both sides of the equation: $2y\frac{dy}{dx}=-x$

Divide both sides of the equation by 2y: $\frac{dy}{dx}=\frac{-x}{2y}$

Plug in the x and y values from the point $(1,\frac{\sqrt{14}}{2})$ into the equation, to calculate the slope of the tangent line: $\frac{dy}{dx}=\frac{-1}{\frac{2\sqrt{14}}{2}}=\frac{-1}{\sqrt{14}}=\frac{-\sqrt{14}}{14}$

Take the negative reciprocal of the slope of the tangent line to calculate the slope of the normal line: $m=-\frac{1}{\frac{-\sqrt{14}}{14}}=\sqrt{14}$

Plug the slope of the normal line into point slope form: $y-\frac{\sqrt{14}}{2}=(x-1)\sqrt{14}$

Add $\frac{\sqrt{14}}{2}$ to both sides to isolate y: $y=(x-1)\sqrt{14}+\frac{\sqrt{14}}{2}$

Simplify the equation: $y=x\sqrt{14}-\sqrt{14}+\frac{\sqrt{14}}{2}$

Simplify further: $y=x\sqrt{14}-\frac{\sqrt{14}}{2}$

Solution: $y=x\sqrt{14}-\frac{\sqrt{14}}{2}$

Report an Error

Example Question #1 : Trapezoidal Sums

$\begin{align*}&\text{Using the method of trapezoidal sums approximate the integral:}\\&\int_{-4}^{1.4}(11sin(17cos(x)))dx\\&\text{Using }2\text{ intervals.}\end{align*}$

Possible Answers:

-63.97

-3.29

-10.84

-105.17

Correct answer:

-10.84

Explanation:

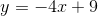
$\begin{align*}&\text{A trapezoidal integral approximation over an interval [a, b]}\\&\text{with n subintervals follows the form:}\\&\int_a^b f(x)dx \approx\sum_{i=1}^{n}\frac{b-a}{n}\frac{f(x_{i+1})+f(x_i)}{2}=\frac{b-a}{2n}(f(x_1)+2f(x_2)+2f(x_3)+...+f(x_n))\\&\text{It is essentially a sum of n trapezoids, each with a base of}\\&\text{length :}\frac{b-a}{n}\text{ and variable paired heights :}f(x_i),f(x_{i+1})\text{, which depend on the function values at }x_i,x_{i+1}\\&\text{We're asked to approximate}\int_{-4}^{1.4}(11sin(17cos(x)))dx\\&\text{So the interval is }[-4,1.4]\text{ the subintervals have length }\frac{1.4-(-4)}{2}=\frac{27}{10}\\&\text{and the x-values are:}\\&[-4,-\frac{13}{10},\frac{7}{5}]\\&\int_{-4}^{1.4}(11sin(17cos(x)))dx\approx\frac{27}{20}[(11sin(17cos((-4))))+2(11sin(17cos((-\frac{13}{10}))))+(11sin(17cos((\frac{7}{5}))))]\\&\int_{-4}^{1.4}(11sin(17cos(x)))dx\approx-10.84\end{align*}$

Report an Error

Example Question #2 : Trapezoidal Sums

$\begin{align*}&\text{Calculate the trapezoidal sums integral approximation of :}\\&\int_{0}^{2}(6cos(20e^{(x)}))dx\\&\text{Using points over }2\text{ intervals.}\end{align*}$

Possible Answers:

-1.68

-0.60

-0.90

-5.20

Correct answer:

-5.20

Explanation:

$\begin{align*}&\text{A trapezoidal integral approximation over an interval [a, b]}\\&\text{with n subintervals follows the form:}\\&\int_a^b f(x)dx \approx\sum_{i=1}^{n}\frac{b-a}{n}\frac{f(x_{i+1})+f(x_i)}{2}=\frac{b-a}{2n}(f(x_1)+2f(x_2)+2f(x_3)+...+f(x_n))\\&\text{It is essentially a sum of n trapezoids, each with a base of}\\&\text{length :}\frac{b-a}{n}\text{ and variable paired heights :}f(x_i),f(x_{i+1})\text{, which depend on the function values at }x_i,x_{i+1}\\&\text{We're asked to approximate}\int_{0}^{2}(6cos(20e^{(x)}))dx\\&\text{So the interval is }[0,2]\text{ the subintervals have length }\frac{2-(0)}{2}=1\\&\text{and the x-values are:}\\&[0,1,2]\\&\int_{0}^{2}(6cos(20e^{(x)}))dx\approx\frac{1}{2}[(6cos(20e^{((0))}))+2(6cos(20e^{((1))}))+(6cos(20e^{((2))}))]\\&\int_{0}^{2}(6cos(20e^{(x)}))dx\approx-5.20\end{align*}$

Report an Error

Example Question #3 : Trapezoidal Sums

$\begin{align*}&\text{Using }3\text{ intervals, and the method of trapezoidal sums approximate the integral:}\\&\int_{-1}^{8.9}(5sin(9e^{(x)}))dx\end{align*}$

Possible Answers:

35.68

6.37

4.20

114.16

Correct answer:

35.68

Explanation:

$\begin{align*}&\text{A trapezoidal integral approximation over an interval [a, b]}\\&\text{with n subintervals follows the form:}\\&\int_a^b f(x)dx \approx\sum_{i=1}^{n}\frac{b-a}{n}\frac{f(x_{i+1})+f(x_i)}{2}=\frac{b-a}{2n}(f(x_1)+2f(x_2)+2f(x_3)+...+f(x_n))\\&\text{It is essentially a sum of n trapezoids, each with a base of}\\&\text{length :}\frac{b-a}{n}\text{ and variable paired heights :}f(x_i),f(x_{i+1})\text{, which depend on the function values at }x_i,x_{i+1}\\&\text{We're asked to approximate}\int_{-1}^{8.9}(5sin(9e^{(x)}))dx\\&\text{So the interval is }[-1,8.9]\text{ the subintervals have length }\frac{8.9-(-1)}{3}=\frac{33}{10}\\&\text{and the x-values are:}\\&[-1,\frac{23}{10},\frac{28}{5},\frac{89}{10}]\\&\int_{-1}^{8.9}(5sin(9e^{(x)}))dx\approx\frac{33}{20}[(5sin(9e^{((-1))}))+2(5sin(9e^{((\frac{23}{10}))}))+2(5sin(9e^{((\frac{28}{5}))}))+(5sin(9e^{((\frac{89}{10}))}))]\\&\int_{-1}^{8.9}(5sin(9e^{(x)}))dx\approx35.68\end{align*}$

Report an Error

Example Question #4 : Trapezoidal Sums

$\begin{align*}&\text{Using the method of trapezoidal sums approximate the integral:}\\&\int_{1}^{6.4}(-6cos(19x^{2}))dx\\&\text{Using }3\text{ intervals.}\end{align*}$

Possible Answers:

-16.73

-33.45

-93.67

-138.84

Correct answer:

-16.73

Explanation:

$\begin{align*}&\text{A trapezoidal integral approximation over an interval [a, b]}\\&\text{with n subintervals follows the form:}\\&\int_a^b f(x)dx \approx\sum_{i=1}^{n}\frac{b-a}{n}\frac{f(x_{i+1})+f(x_i)}{2}=\frac{b-a}{2n}(f(x_1)+2f(x_2)+2f(x_3)+...+f(x_n))\\&\text{It is essentially a sum of n trapezoids, each with a base of}\\&\text{length :}\frac{b-a}{n}\text{ and variable paired heights :}f(x_i),f(x_{i+1})\text{, which depend on the function values at }x_i,x_{i+1}\\&\text{We're asked to approximate}\int_{1}^{6.4}(-6cos(19x^{2}))dx\\&\text{So the interval is }[1,6.4]\text{ the subintervals have length }\frac{6.4-(1)}{3}=\frac{9}{5}\\&\text{and the x-values are:}\\&[1,\frac{14}{5},\frac{23}{5},\frac{32}{5}]\\&\int_{1}^{6.4}(-6cos(19x^{2}))dx\approx\frac{9}{10}[(-6cos(19(1)^{2}))+2(-6cos(19(\frac{14}{5})^{2}))+2(-6cos(19(\frac{23}{5})^{2}))+(-6cos(19(\frac{32}{5})^{2}))]\\&\int_{1}^{6.4}(-6cos(19x^{2}))dx\approx-16.73\end{align*}$

Report an Error

Example Question #5 : Trapezoidal Sums

$\begin{align*}&\text{Using the method of trapezoidal sums approximate the integral:}\\&\int_{2}^{6.5}(17cos(2sin(2x)))dx\\&\text{Using }3\text{ intervals.}\end{align*}$

Possible Answers:

5.51

3.13

7.65

27.55

Correct answer:

27.55

Explanation:

$\begin{align*}&\text{A trapezoidal integral approximation over an interval [a, b]}\\&\text{with n subintervals follows the form:}\\&\int_a^b f(x)dx \approx\sum_{i=1}^{n}\frac{b-a}{n}\frac{f(x_{i+1})+f(x_i)}{2}=\frac{b-a}{2n}(f(x_1)+2f(x_2)+2f(x_3)+...+f(x_n))\\&\text{It is essentially a sum of n trapezoids, each with a base of}\\&\text{length :}\frac{b-a}{n}\text{ and variable paired heights :}f(x_i),f(x_{i+1})\text{, which depend on the function values at }x_i,x_{i+1}\\&\text{We're asked to approximate}\int_{2}^{6.5}(17cos(2sin(2x)))dx\\&\text{So the interval is }[2,6.5]\text{ the subintervals have length }\frac{6.5-(2)}{3}=\frac{3}{2}\\&\text{and the x-values are:}\\&[2,\frac{7}{2},5,\frac{13}{2}]\\&\int_{2}^{6.5}(17cos(2sin(2x)))dx\approx\frac{3}{4}[(17cos(2sin(2(2))))+2(17cos(2sin(2(\frac{7}{2}))))+2(17cos(2sin(2(5))))+(17cos(2sin(2(\frac{13}{2}))))]\\&\int_{2}^{6.5}(17cos(2sin(2x)))dx\approx27.55\end{align*}$

Report an Error

Example Question #6 : Trapezoidal Sums

$\begin{align*}&\text{Using the method of trapezoidal sums approximate the integral:}\\&\int_{0}^{4.4}(-196cos(3x)^{2})dx\\&\text{Using }2\text{ intervals.}\end{align*}$

Possible Answers:

-2160.41

-88.69

-130.70

-744.97

Correct answer:

-744.97

Explanation:

$\begin{align*}&\text{A trapezoidal integral approximation over an interval [a, b]}\\&\text{with n subintervals follows the form:}\\&\int_a^b f(x)dx \approx\sum_{i=1}^{n}\frac{b-a}{n}\frac{f(x_{i+1})+f(x_i)}{2}=\frac{b-a}{2n}(f(x_1)+2f(x_2)+2f(x_3)+...+f(x_n))\\&\text{It is essentially a sum of n trapezoids, each with a base of}\\&\text{length :}\frac{b-a}{n}\text{ and variable paired heights :}f(x_i),f(x_{i+1})\text{, which depend on the function values at }x_i,x_{i+1}\\&\text{We're asked to approximate}\int_{0}^{4.4}(-196cos(3x)^{2})dx\\&\text{So the interval is }[0,4.4]\text{ the subintervals have length }\frac{4.4-(0)}{2}=\frac{11}{5}\\&\text{and the x-values are:}\\&[0,\frac{11}{5},\frac{22}{5}]\\&\int_{0}^{4.4}(-196cos(3x)^{2})dx\approx\frac{11}{10}[(-196cos(3(0))^{2})+2(-196cos(3(\frac{11}{5}))^{2})+(-196cos(3(\frac{22}{5}))^{2})]\\&\int_{0}^{4.4}(-196cos(3x)^{2})dx\approx-744.97\end{align*}$

Report an Error

Example Question #7 : Trapezoidal Sums

$\begin{align*}&\text{Using }3\text{ intervals, and the method of trapezoidal sums approximate the integral:}\\&\int_{3}^{7.2}(11cos(6e^{(4x)}))dx\end{align*}$

Possible Answers:

-0.56

-18.44

-1.86

-0.29

Correct answer:

-1.86

Explanation:

$\begin{align*}&\text{A trapezoidal integral approximation over an interval [a, b]}\\&\text{with n subintervals follows the form:}\\&\int_a^b f(x)dx \approx\sum_{i=1}^{n}\frac{b-a}{n}\frac{f(x_{i+1})+f(x_i)}{2}=\frac{b-a}{2n}(f(x_1)+2f(x_2)+2f(x_3)+...+f(x_n))\\&\text{It is essentially a sum of n trapezoids, each with a base of}\\&\text{length :}\frac{b-a}{n}\text{ and variable paired heights :}f(x_i),f(x_{i+1})\text{, which depend on the function values at }x_i,x_{i+1}\\&\text{We're asked to approximate}\int_{3}^{7.2}(11cos(6e^{(4x)}))dx\\&\text{So the interval is }[3,7.2]\text{ the subintervals have length }\frac{7.2-(3)}{3}=\frac{7}{5}\\&\text{and the x-values are:}\\&[3,\frac{22}{5},\frac{29}{5},\frac{36}{5}]\\&\int_{3}^{7.2}(11cos(6e^{(4x)}))dx\approx\frac{7}{10}[(11cos(6e^{(4(3))}))+2(11cos(6e^{(4(\frac{22}{5}))}))+2(11cos(6e^{(4(\frac{29}{5}))}))+(11cos(6e^{(4(\frac{36}{5}))}))]\\&\int_{3}^{7.2}(11cos(6e^{(4x)}))dx\approx-1.86\end{align*}$

Report an Error

View AP Calculus AB Tutors

Jozsef
Certified Tutor

University of Waterloo, Doctor of Philosophy, Applied Mathematics.

View AP Calculus AB Tutors

Laura
Certified Tutor

University of Cincinnati, Bachelor in Arts, Mathematics. University of Cincinnati, Master of Science, Mathematics.

View AP Calculus AB Tutors

Satweka
Certified Tutor

The University of Texas at Dallas, Master of Science, Biomedical Engineering.

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

French Tutors in Houston, Statistics Tutors in Los Angeles, Calculus Tutors in Miami, Reading Tutors in San Diego, ACT Tutors in Dallas Fort Worth, SAT Tutors in Denver, LSAT Tutors in Miami, English Tutors in Boston, Physics Tutors in Dallas Fort Worth, Math Tutors in Washington DC

Popular Courses & Classes

Spanish Courses & Classes in Chicago, SAT Courses & Classes in Chicago, ACT Courses & Classes in Atlanta, SAT Courses & Classes in Houston, ISEE Courses & Classes in Los Angeles, LSAT Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Atlanta, SSAT Courses & Classes in Philadelphia, GMAT Courses & Classes in San Diego, SAT Courses & Classes in Philadelphia

Popular Test Prep

LSAT Test Prep in Denver, GRE Test Prep in Miami, SAT Test Prep in Washington DC, SSAT Test Prep in Chicago, MCAT Test Prep in Atlanta, MCAT Test Prep in Dallas Fort Worth, ACT Test Prep in Atlanta, ISEE Test Prep in San Francisco-Bay Area, GRE Test Prep in Phoenix, LSAT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #21 : Implicit Differentiation

Example Question #21 : Implicit Differentiation

Example Question #31 : Implicit Differentiation

Example Question #1 : Trapezoidal Sums

Example Question #2 : Trapezoidal Sums

Example Question #3 : Trapezoidal Sums

Example Question #4 : Trapezoidal Sums

Example Question #5 : Trapezoidal Sums

Example Question #6 : Trapezoidal Sums

Example Question #7 : Trapezoidal Sums

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: