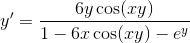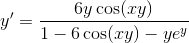Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Implicit Differentiation

Find $\frac{\mathrm{d} \alpha}{\mathrm{d} x}$ , where $\alpha$ is a function of x:

$\alpha^2x^2+2\alpha x=\alpha$

Possible Answers:

$\frac{2\alpha^2 x+2 \alpha}{1+2\alpha x^2+2x}$

$\frac{2\alpha^2 x+2 \alpha}{1-2\alpha x^2 -2x}$

$\frac{2\alpha x^2+2 \alpha}{1-2\alpha^2 x -2x}$

None of the other answers

Correct answer:

$\frac{2\alpha^2 x+2 \alpha}{1-2\alpha x^2 -2x}$

Explanation:

To find the derivative of $\alpha$ with respect to x, we must take the differentiate both sides of the equation with respect to x:

$2\alpha x^2 \frac{\mathrm{d} \alpha}{\mathrm{d} x}+2\alpha^2x+2x \frac{\mathrm{d} \alpha}{\mathrm{d} x}+2x=\frac{\mathrm{d} \alpha}{\mathrm{d} x}$

The following derivative rules were used:

$\frac{\mathrm{d} }{\mathrm{d} x} f(g(x))=f'(g(x))\cdot g'(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} f(x)g(x)=f'(x)g(x)+f(x)g'(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$ , $\frac{\mathrm{d} }{\mathrm{d} x} ax=a$

Note that the chain rule was used for the derivative of any function containing $\alpha$ , whose derivative with respect to x we want to solve for.

Solving, we get

$\frac{\mathrm{d} \alpha}{\mathrm{d} x}=\frac{2\alpha^2 x+2 \alpha}{1-2\alpha x^2 -2x}$

Report an Error

Example Question #1 : Implicit Differentiation

Given that y=y(x) , find the derivative of the function

$y=\sin(xy)+\tan(y^2)$

Possible Answers:

$y'=\frac{y\cos(xy)}{1-x\cos(xy)-2y\sec^2(y^2)}$

$y'=\frac{y\cos(xy)}{1-x\cos(xy)-y\sec^2(y^2)}$

$y'=\frac{y\cos(x)}{1-x\cos(xy)-2y\sec^2(y^2)}$

$y'=\frac{x\cos(xy)}{1-x\cos(xy)-\sec^2(y^2)}$

Correct answer:

$y'=\frac{y\cos(xy)}{1-x\cos(xy)-2y\sec^2(y^2)}$

Explanation:

To solve this using implicit differentiation, we must always treat y as a function of x, and therefore when we differentiate y with respect to x, we denote it as

Step by step, we get the following:

$y'=\cos(xy)(y+xy')+\sec^2(y^2)(2yy')$

This resulted from the product rule and chain rule

The next steps are:

$y'=y\cos(xy)+xy'\cos(xy)+2yy'\sec^2(y^2)$

$y'-xy'\cos(xy)-2yy'\sec^2(y^2)=y\cos(xy)$

$y'(1-x\cos(xy)-2y\sec^2(y^2))=y\cos(xy)$

$y'=\frac{y\cos(xy)}{1-x\cos(xy)-2y\sec^2(y^2)}$

Report an Error

Example Question #11 : Implicit Differentiation

Given that y=y(x) , find the derivative of the following function:

$y=y\cos(x^3)$

Possible Answers:

$y'=\frac{-3x^2y\sin(x^3)}{1-\cos(x^2)}$

$y'=\frac{3x^2y\sin(x^3)}{1-\cos(y^3)}$

$y'=\frac{-3x^2y\sin(x^3)}{1-\cos(x^3)}$

$y'=\frac{-3x^2y\sin(x^3)}{1+\sin(x^3)}$

Correct answer:

$y'=\frac{-3x^2y\sin(x^3)}{1-\cos(x^3)}$

Explanation:

To find the derivative of the function, we use implicit differentiation, where we always treat y as a function of x, and denoting any derivative of y with respect to x as

$y'=y'\cos(x^3)-3x^2y\sin(x^3)$

$y'-y'\cos(x^3)=-3x^2y\sin(x^3)$

$y'(1-\cos(x^3))=-3x^2y\sin(x^3)$

$y'=\frac{-3x^2y\sin(x^3)}{1-\cos(x^3)}$

Report an Error

Example Question #591 : Derivatives

Find $\frac{\mathrm{d} y}{\mathrm{d} x}$ from the following equation:

$e^{2y}+x^2y^2=y$

Possible Answers:

$-\frac{2e^{2y}+2x^2y-1}{2xy^2}$

$\frac{-2xy^2-2x^2y}{2e^{2y}-1}$

$\frac{-2xy^2}{2e^{2y}+2x^2y-1}$

$\frac{2xy^2}{2e^{2y}+2x^2y-1}$

Correct answer:

$\frac{-2xy^2}{2e^{2y}+2x^2y-1}$

Explanation:

To find the derivative of y with respect to x, we must take the derivative with respect to x of both sides of the equation:

$2e^{2y}\frac{\mathrm{d} y}{\mathrm{d} x}+2xy^2+2x^2y\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{\mathrm{d} y}{\mathrm{d} x}$

The derivatives were found using the following rules:

$\frac{\mathrm{d} }{\mathrm{d} x} f(g(x))=f'(g(x))\cdot g'(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} e^u=e^u\frac{\mathrm{d} u}{\mathrm{d} x}$ , $\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$

Notice the chain rule was used for every function containing y, because y is a function of x and its whose derivative we are interested in isolating.

Using algebra to solve, our final answer is

$\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{-2xy^2}{2e^{2y}+2x^2y-1}$

Report an Error

Example Question #11 : Implicit Differentiation

Find $\frac{\mathrm{d} y}{\mathrm{d} x}$ :

$y^4=\sin(2x)$

Possible Answers:

$-\frac{\cos(2x)}{2y^3}$

$\frac{\cos(2x)}{2y^3}$

$\frac{4\cos(2x)}{y^3}$

$2\cos(2x)$

Correct answer:

$\frac{\cos(2x)}{2y^3}$

Explanation:

To find $\frac{\mathrm{d} y}{\mathrm{d} x}$ we must use implicit differentiation, which is an application of the chain rule.

Taking $\frac{\mathrm{d} }{\mathrm{d} x}$ of both sides of the equation, we get

$4y^3 \frac{\mathrm{d} y}{\mathrm{d} x}=2\cos(2x)$

The derivatives were found using the following rules:

$\frac{\mathrm{d} }{\mathrm{d} x} f(g(x))=f'(g(x))\cdot g'(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$ , $\frac{\mathrm{d} }{\mathrm{d} x} \sin(x)=\cos(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} ax=a$

Note that for every derivative of a function with y, the additional term $\frac{\mathrm{d} y}{\mathrm{d} x}$ appears; this is because of the chain rule, where y=g(x), so to speak, for the function it appears in.

Solving for $\frac{\mathrm{d} y}{\mathrm{d} x}$ , we get

$\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{\cos(2x)}{2y^3}$

Report an Error

Example Question #63 : Applications Of Derivatives

Evaluate $\frac{\mathrm{d}y }{\mathrm{d} x}$ at the point (1, 4) for the following equation:

xy + 3x^2 - 2y^2 = -25 .

Possible Answers:

$\frac{2}{3}$

$\frac{15}{2}$

$-\frac{2}{3}$

$\frac{3}{2}$

$\frac{2}{15}$

Correct answer:

$\frac{2}{3}$

Explanation:

Using implicit differentiation, taking the derivative of the given equation yields

$y + \frac{\mathrm{d} y}{\mathrm{d} x}x + 6x -4y\frac{\mathrm{d} y}{\mathrm{d} x} = 0$

Getting all the $\frac{\mathrm{d} y}{\mathrm{d} x}$ 's to their own side, we have

$x\frac{\mathrm{d} y}{\mathrm{d} x} - 4y\frac{\mathrm{d} y}{\mathrm{d} x} = -6x - y$

Factoring,

$\frac{\mathrm{d} y}{\mathrm{d} x}(x - 4y) = -6x - y$

And dividing

$\frac{\mathrm{d}y }{\mathrm{d} x} = \frac{-6x - y}{x - 4y}$

Plugging in our point, (1, 4) , we have

$\frac{\mathrm{d} y}{\mathrm{d} x} = \frac{-6 - 4}{1 - 16} = \frac{-10}{-15} =\frac{2}{3}$

Report an Error

Example Question #64 : Applications Of Derivatives

Determine $\frac{\mathrm{d} y}{\mathrm{d} x}$ :

$y^3+\sec(y)=3x^2$

Possible Answers:

$\frac{6x}{3y^2+\sec^2(y)}$

$\frac{3y^2+\sec(y)\tan(y)}{6x}$

$\frac{6x+3y^2}{\sec(y)\tan(y)}$

$\frac{6x}{3y^2+\sec(y)\tan(y)}$

Correct answer:

$\frac{6x}{3y^2+\sec(y)\tan(y)}$

Explanation:

To find $\frac{\mathrm{d} y}{\mathrm{d} x}$ we must use implicit differentiation, which is an application of the chain rule.

Taking the derivative with respect to x of both sides of the equation, we get

$3y^2 \frac{\mathrm{d} y}{\mathrm{d} x}+\sec(y)\tan(y)\frac{\mathrm{d} y}{\mathrm{d} x}=6x$

The derivatives were found using the following rules:

$\frac{\mathrm{d} }{\mathrm{d} x} f(g(x))=f'(g(x))\cdot g'(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} \sec(x)=\sec(x)\tan(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$

Using algebra to solve for $\frac{\mathrm{d} y}{\mathrm{d} x}$ , we get

$\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{6x}{3y^2+\sec(y)\tan(y)}$

Report an Error

Example Question #65 : Applications Of Derivatives

Find $\frac{\mathrm{d} y}{\mathrm{d} x}$ :

ye^y+x=2xy

Possible Answers:

$\frac{2y-1}{e^y-2x}$

$\frac{2y-1}{e^y-ye^y-2x}$

$\frac{2y-1+e^y}{-ye^y-2x}$

$\frac{2y-1+2x}{e^y-ye^y}$

Correct answer:

$\frac{2y-1}{e^y-ye^y-2x}$

Explanation:

To find $\frac{\mathrm{d} y}{\mathrm{d} x}$ we must use implicit differentiation, which is an application of the chain rule.
Taking $\frac{\mathrm{d} }{\mathrm{d} x}$ of both sides of the equation, we get

$e^y \frac{\mathrm{d} y}{\mathrm{d} x}+ye^y\frac{\mathrm{d} y}{\mathrm{d} x}+1=2y+2x\frac{\mathrm{d} y}{\mathrm{d} x}$

which was found using the following rules:

Using algebra to solve for $\frac{\mathrm{d} y}{\mathrm{d} x}$ , we get

$\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{2y-1}{e^y-ye^y-2x}$

Report an Error

Example Question #66 : Applications Of Derivatives

Given that y=y(x) , compute the derivative of the following function

$y=6\sin(xy)+e^y$

Possible Answers:

$y'=\frac{6y\cos(xy)}{1+6\cos(xy)-e^y}$

$y'=\frac{6y\cos(xy)}{1-6x\cos(xy)-e^y}$

$y'=\frac{6y\cos(xy)}{1-6\cos(xy)-ye^y}$

$y'=\frac{6y\sin(xy)}{1-6\cos(xy)-e^y}$

Correct answer:

$y'=\frac{6y\cos(xy)}{1-6x\cos(xy)-e^y}$

Explanation:

To find the derivative of the function, we use implicit differentiation, which is an application of the chain rule. We use this because y=y(x) , and any derivative with respect to is $\frac{\mathrm{d} y}{\mathrm{d} x}$ (or ).

First, we use the chain rule combined with the product rule in taking the derivative of y

$y'=6\cos(xy)(xy'+y)+y'e^y$

Then we expand in order to isolate the terms with

$y'=6xy'\cos(xy)+6y\cos(xy)+y'e^y$

$y'-6xy'\cos(xy)-y'e^y=6y\cos(xy)$

Then we factor out a

$y'(1-6x\cos(xy)-e^y)=6y\cos(xy)$

$y'=\frac{6y\cos(xy)}{1-6x\cos(xy)-e^y}$

Report an Error

Example Question #71 : Applications Of Derivatives

Given that y=y(x) , compute the derivative of the following function:

$y=xy^2+4\sin(y)$

Possible Answers:

$y'=\frac{y^2}{1+2xy-4\cos(y)}$

$y'=\frac{y^2}{1-2xy-4\cos(y)}$

$y'=\frac{y^2}{1-2xy-4\sin(y)}$

$y'=\frac{2y^2}{1-2xy-4\cos(y)}$

Correct answer:

$y'=\frac{y^2}{1-2xy-4\cos(y)}$

Explanation:

First, we use the chain rule combined with the product rule in taking the derivative of y

$y'=y^2+x(2y)(y')+4\cos(y)(y')$

Then isolate the terms with

$y'-2xyy'-4y'\cos(y)=y^2$

Then we factor out a

$y'(1-2xy-4\cos(y))=y^2$

$y'=\frac{y^2}{1-2xy-4\cos(y)}$

Report an Error

View AP Calculus AB Tutors

Vikash
Certified Tutor

national institute of technology Jamshedpur , Bachelor, Civil engineering .

View AP Calculus AB Tutors

Damion
Certified Tutor

Saint Edward's University, Bachelors, Accounting. The University of Texas at Austin, Master of Science, Accounting.

View AP Calculus AB Tutors

Jeremy
Certified Tutor

University of Illinois at Chicago, Bachelor of Science, Physics.

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ISEE Tutors in Washington DC, ISEE Tutors in Philadelphia, ACT Tutors in Boston, MCAT Tutors in San Francisco-Bay Area, Biology Tutors in Dallas Fort Worth, Algebra Tutors in Seattle, Chemistry Tutors in Denver, GRE Tutors in San Francisco-Bay Area, Statistics Tutors in San Diego, GRE Tutors in Dallas Fort Worth

Popular Courses & Classes

ISEE Courses & Classes in New York City, ISEE Courses & Classes in Phoenix, GRE Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Seattle, GMAT Courses & Classes in Seattle, MCAT Courses & Classes in Los Angeles, SSAT Courses & Classes in New York City, GRE Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Chicago, ISEE Courses & Classes in Dallas Fort Worth

Popular Test Prep

LSAT Test Prep in Washington DC, SAT Test Prep in San Diego, ACT Test Prep in Denver, MCAT Test Prep in Washington DC, LSAT Test Prep in New York City, SSAT Test Prep in Phoenix, SSAT Test Prep in Denver, LSAT Test Prep in Boston, GMAT Test Prep in Washington DC, MCAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #1 : Implicit Differentiation

Example Question #1 : Implicit Differentiation

Example Question #11 : Implicit Differentiation

Example Question #591 : Derivatives

Example Question #11 : Implicit Differentiation

Example Question #63 : Applications Of Derivatives

Example Question #64 : Applications Of Derivatives

Example Question #65 : Applications Of Derivatives

Example Question #66 : Applications Of Derivatives

Example Question #71 : Applications Of Derivatives

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: