To solve for , we must first solve the equation with the complex number for  and . We therefore need to match up the real portion of the compex number with the real portions of the expression, and the imaginary portion of the complex number with the imaginary portion of the expression. We therefore obtain:

 and 

We can use substitution by noticing the first equation can be rewritten as  and substituting it into the second equation. We can therefore solve for :

With this  value, we can solve for :

Since we now have  and , we can solve for :

Our final answer is therefore 

Go about this problem just like any other algebra problem by following your order of operations. We will first evaluate what is inside the parentheses: . At this point, we need to know the properties of  which are as follows:

Therefore,  and the original expression becomes  

The first step is to evaluate the expression. By FOILing the expression, we get:

Now we need to simplify any terms that we can by using the properties of 

Therefore, the expression becomes

In order to solve this problem, we need to first simplify our equation. The first thing we should do is distribute the square, which gives us

Now  is actually just . Therefore, this becomes

Now all we need to do is solve for  in the equation:

which gives us

Finally, we get 

and therefore, our solution is

Remember that 

So the powers of  are cyclic. This means that when we try to figure out the value of an exponent of , we can ignore all the powers that are multiples of  because they end up multiplying the end result by , and therefore do nothing.

This means that 

Now, remembering the relationships of the exponents of , we can simplify this to:

Because the elements on the left and right have to correspond (no mixing and matching!), we get the relationships: 

No matter how you solve it, you get the values , .

To solve

Subtract  from both side:

Which is never true, so there is no solution.

Use the change of base formula for logarithmic functions and incorporate the fact that  and 

Or

 can be solved using 

Imaginary numbers do not fall on the number line-- they are by definition not real numbers. 

** If the question asked where  falls on the number line, the answer would be to the left of 0, because .

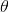
To see what the polar form of the number is, it helps to draw it on a graph, where the horizontal axis is the imaginary part and the vertical axis the real part. This is called the complex plane.

To find the angle , we can find its supplementary angle  and subtract it from  radians, so .

Using trigonometric ratios, 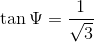   and  .

Then .

To find the distance , we need to find the distance from the origin to the point . Using the Pythagorean Theorem to find the hypotenuse ,  or .

 Imaginary numbers do not fall on the number line by definition, since they are not real numbers. However, although i is an imaginary number equal to the square root of -1,  is a real number since . Therefore, . Negative numbers fall to the left of 0 on a number line.