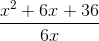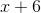In order to subtract the fractions, we will need to determine the least common denominator.

Multiply the second fraction's numerator and denominator by ten, since both fractions share an x-term.

Combine the numerator to form one fraction.

The answer is:  

In order to add the numerators, we will need to find the least common denominator.

Use the FOIL method to multiply the two denominators together.

Simplify by combining like-terms.  The LCD is:  

Change the fractions.

Simplify the fractions.

Combine like-terms.

The answer is:  

Determine the least common denominator in order to add the numerator.

Each denominator shares an  term.  The least common denominator is  since it is divisible by each coefficient of the denominator.

Convert the fractions.

Simplify the top and bottom.

The answer is:  

Determine the least common denominator.  Each term will need an x-variable, and all three denominators will need a common coefficient.

The least common denominator is .

Convert the fractions.

The expression becomes: 

The answer is:  

Notice that  can be factorized by the difference of squares.  This means that the second fraction will need to multiply the quantity of  in order for the denominators to be similar.

Convert the fractions.

Simplify the fractions and combine as one fraction.  

The expression becomes:

Combine like-terms.

Factor out a negative one from the numerator to pull the negative sign in front of the fraction.

The answer is:  

In order to add the numerators in this expression, we will need to calculate the least common denominator. In this case, the least common denominator is . Let's multiply the fraction on the left by a value of one. Let's start with the left expression. We will multiply it by one in the following form:

Now convert the right fraction to a form with the same denominator. Again, multiply the fraction by a value of one in the following form:

Now, we can add our two fractions by rewriting them as one whole fraction.

Simplify the numerator.

This cannot be reduced or simplified any further; therefore, the answer is:

To find the slant asymptote, we have to divide the numerator by the denominator and see the equation of the line that we get.

Our long division problem ends up looking like this:

(We can ignore the remainder because it doesn't sufficiently impact the equation of the asymptote, especially as approaches infinity.)

Thus, the equation of the slant asymptote is .

Our first step in this problem would be to distribute the exponent on the second term, which makes the expression become:

We then multiply like terms, remembering that multiplying like terms with exponents means we will add the exponent, so the expression becomes:

a. Like when dividing fractions, change the division sign to multiplication and use the reciprocal of the divisor. 

b. Factor the trinomials in the numerator of both terms.

c. Cancel any common factors between the numerators and denominators.

This will leave: 

d. Multiply to simplify.